这篇文章主要为大家详细介绍了java计算图两点之间的所有路径,具有一定的参考价值,感兴趣的小伙伴们可以参考一下
本文实例为大家分享了java计算图两点之间的所有路径的具体代码,供大家参考,具体内容如下
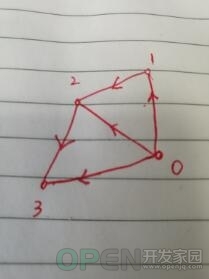
1.给定图如下:
2.求0到3之间可达的所有路径
这里问题就是关于搜索遍历的问题,但其中需要注意到不能产生回路或环.
算法描述如下:
top_node:当前栈顶元素
adjvex_node;当前top_node已经访问的邻接点
next_node:即将访问的元素(top_node的第adjvex_node个邻接点所对应的元素)
找出所有路径采用的是遍历的方法,以“深度优先”算法为基础。从源点出发,先到源点的第一个邻接点n00,再到n00的第一个邻接点n10,再到n10的第一个邻接点n20...当遍历到目标点时表明找到一条路径。
上述代码的核心数据结构为一个栈,主要步骤:
①源点先入栈,并进行标记
②获取栈顶元素top_node,如果栈顶为终点时,即找到一条路径,栈顶元素top_node出栈,此时adjvex_node=top_node,新的栈顶元素为top_node,否则执行③
③从top_node的所有邻接点中,从adjvex_node为起点,选取下一个邻接点next_node;如果该元素非空,则入栈,使得adjvex_node=-1,(adjvex_node=-1代表top_node的邻接点一个还没有访问)做入栈标记。否则代表没有后续节点了,此时必须出栈栈顶元素,并置adjvex_node为该栈顶元素,并做出栈标记。
④为避免回路,已入栈元素要记录,选取新入栈顶点时应跳过已入栈的顶点,当栈为空时,遍历完成
3.java代码实现
1)图结构
点表public class vertex {
//存放点信息
public int data;
//与该点邻接的第一个边节点
public edge firstedge;
}
边表(代表与点相连的点的集合)//边节点
public class edge {
//对应的点下表
public int vertexid;
//边的权重
public int weight;
//下一个边节点
public edge next;
//getter and setter自行补充
}
2).算法实现import java.util.hashmap;
import java.util.map;
import java.util.stack;
public class graph {
public vertex[] vertexlist; //存放点的集合
public graph(int vertexnum){
this.vertexnum=vertexnum;
vertexlist=new vertex[vertexnum];
}
//点个数
public int vertexnum;
//边个数
public int edgelength;
public void initvertext(int datas[]){
for(int i=0;i<vertexnum;i++){
vertex vertext=new vertex();
vertext.data=datas[i];
vertext.firstedge=null;
vertexlist[i]=vertext;
//system.out.println("i"+vertexlist[i]);
}
isvisited=new boolean[vertexnum];
for(int i=0;i<isvisited.length;i++){
isvisited[i]=false;
}
}
//针对x节点添加边节点y
public void addedge(int x,int y,int weight){
edge edge=new edge();
edge.setvertexid(y);
edge.setweight(weight);
//第一个边节点
system.out.println(vertexlist.length);
if(null==vertexlist[x].firstedge){
vertexlist[x].firstedge=edge;
edge.setnext(null);
}
//不是第一个边节点,则采用头插法
else{
edge.next=vertexlist[x].firstedge;
vertexlist[x].firstedge=edge;
}
}
//得到x的邻接点为y的后一个邻接点位置,为-1说明没有找到
public int getnextnode(int x,int y){
int next_node=-1;
edge edge=vertexlist[x].firstedge;
if(null!=edge&&y==-1){
int n=edge.vertexid;
//元素还不在stack中
if(!states.get(n))
return n;
return -1;
}
while(null!=edge){
//节点未访问
if(edge.vertexid==y){
if(null!=edge.next){
next_node=edge.next.vertexid;
if(!states.get(next_node))
return next_node;
}
else
return -1;
}
edge=edge.next;
}
return -1;
}
//代表某节点是否在stack中,避免产生回路
public map<integer,boolean> states=new hashmap();
//存放放入stack中的节点
public stack<integer> stack=new stack();
//输出2个节点之间的输出路径
public void visit(int x,int y){
//初始化所有节点在stack中的情况
for(int i=0;i<vertexnum;i++){
states.put(i,false);
}
//stack top元素
int top_node;
//存放当前top元素已经访问过的邻接点,若不存在则置-1,此时代表访问该top元素的第一个邻接点
int adjvex_node=-1;
int next_node;
stack.add(x);
states.put(x,true);
while(!stack.isempty()){
top_node=stack.peek();
//找到需要访问的节点
if(top_node==y){
//打印该路径
printpath();
adjvex_node=stack.pop();
states.put(adjvex_node,false);
}
else{
//访问top_node的第advex_node个邻接点
next_node=getnextnode(top_node,adjvex_node);
if(next_node!=-1){
stack.push(next_node);
//置当前节点访问状态为已在stack中
states.put(next_node,true);
//临接点重置
adjvex_node=-1;
}
//不存在临接点,将stack top元素退出
else{
//当前已经访问过了top_node的第adjvex_node邻接点
adjvex_node=stack.pop();
//不在stack中
states.put(adjvex_node,false);
}
}
}
}
//打印stack中信息,即路径信息
public void printpath(){
stringbuilder sb=new stringbuilder();
for(integer i :stack){
sb.append(i+"->");
}
sb.delete(sb.length()-2,sb.length());
system.out.println(sb.tostring());
}
public static void main(string[]args){
graph g=new graph(5);
g.initvertext(new int[]{1,2,3,4,4});
//system.out.println(g.vertexlist[0]);
g.addedge(0,1,1);
g.addedge(0,2,3);
g.addedge(0,3,4);
g.addedge(1,2,1);
g.addedge(2,0,1);
g.addedge(2,3,1);
g.addedge(1,3,2);
g.visit(0,3);
}
}
执行结果如下:0->3
0->2->3
0->1->2->3
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持CodeAE代码之家。
原文链接:https://blog.csdn.net/xqhadoop/article/details/66476728
| 
![]() 编程语言
发布于:2021-10-05 20:16
|
阅读数:357
|
评论:0
编程语言
发布于:2021-10-05 20:16
|
阅读数:357
|
评论:0

 QQ好友和群
QQ好友和群 QQ空间
QQ空间