看动画学算法之:平衡二叉搜索树AVL Tree

飞奔的炮台

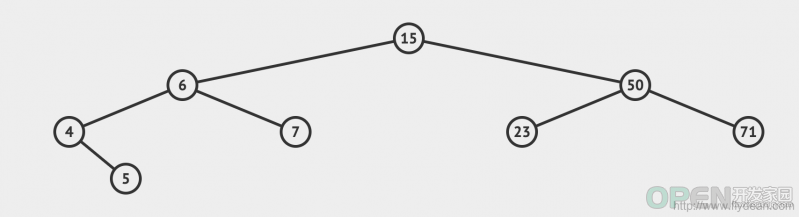
简介
平衡二叉搜索树是一种特殊的二叉搜索树。为什么会有平衡二叉搜索树呢？
考虑一下二叉搜索树的特殊情况，如果一个二叉搜索树所有的节点都是右节点，那么这个二叉搜索树将会退化成为链表。从而导致搜索的时间复杂度变为O(n),其中n是二叉搜索树的节点个数。
而平衡二叉搜索树正是为了解决这个问题而产生的，它通过限制树的高度，从而将时间复杂度降低为O(logn)。
AVL的特性
在讨论AVL的特性之前，我们先介绍一个概念叫做平衡因子，平衡因子表示的是左子树和右子树的高度差。
如果平衡因子=0，表示这是一个完全平衡二叉树。
如果平衡因子=1，那么这棵树就是平衡二叉树AVL。
也就是是说AVL的平衡因子不能够大于1。
先看一个AVL的例子：

总结一下，AVL首先是一个二叉搜索树，然后又是一个二叉平衡树。
AVL的构建
有了AVL的特性之后，我们看下AVL是怎么构建的。

public class AVLTree {
  //根节点
  Node root;
  class Node {
    int data; //节点的数据
    int height; //节点的高度
    Node left;
    Node right;
    public Node(int data) {
      this.data = data;
      left = right = null;
    }
  }

同样的，AVL也是由各个节点构成的，每个节点拥有data，left和right几个属性。
因为是二叉平衡树，节点是否平衡还跟节点的高度有关，所以我们还需要定义一个height作为节点的高度。
在来两个辅助的方法，一个是获取给定的节点高度：

//获取给定节点的高度
  int height(Node node) {
    if (node == null)
      return 0;
    return node.height;
  }

和获取平衡因子：

//获取平衡因子
  int getBalance(Node node) {
    if (node == null)
      return 0;
    return height(node.left) - height(node.right);
  }

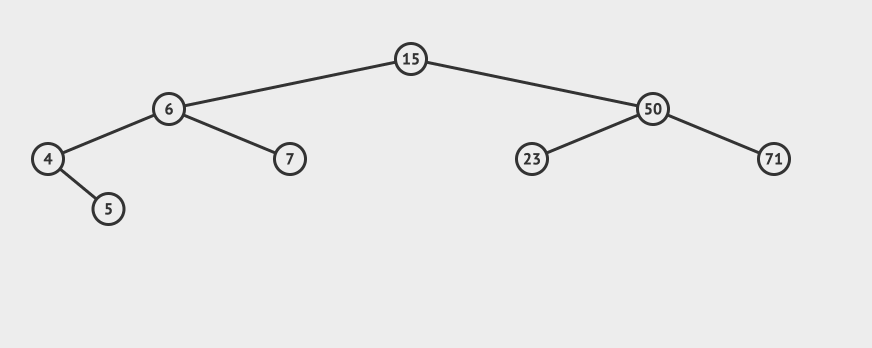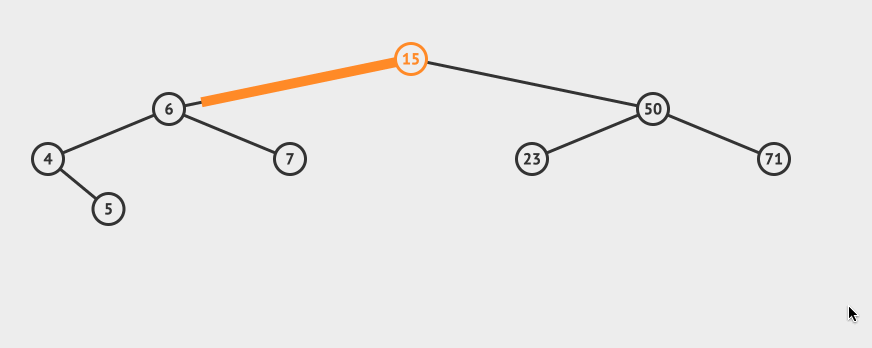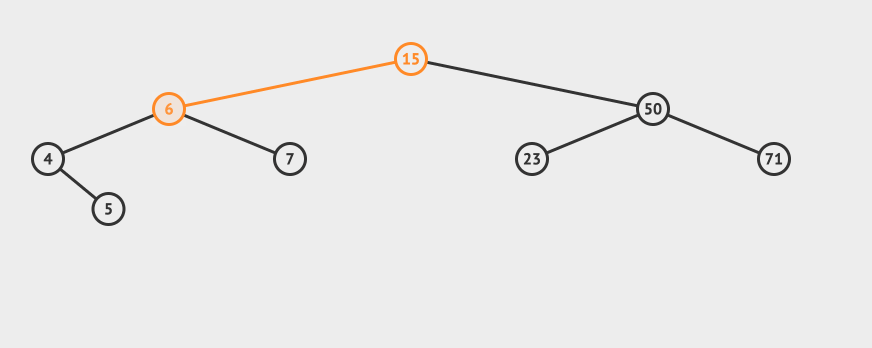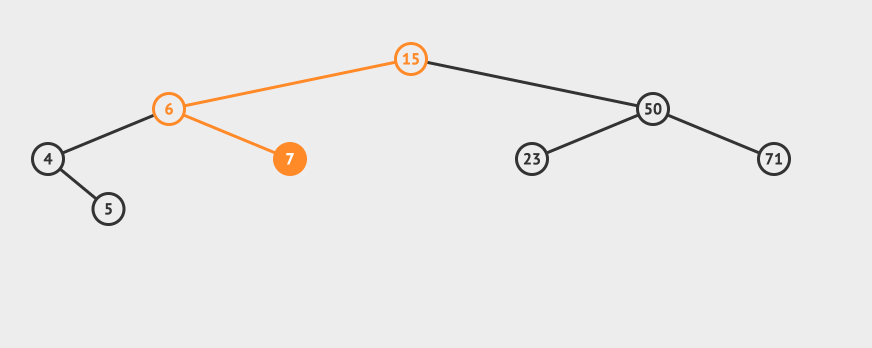
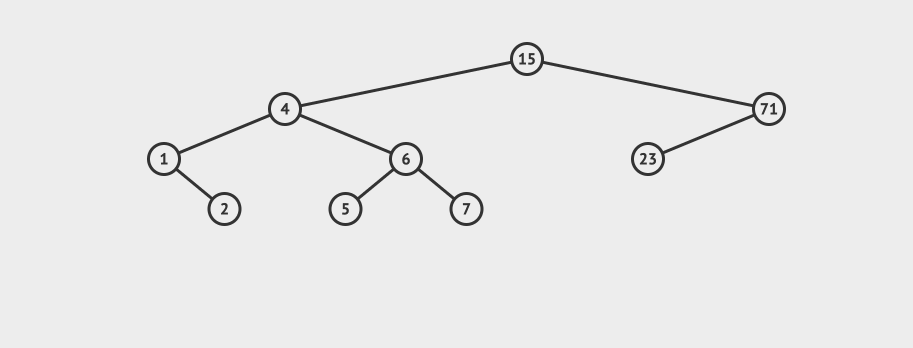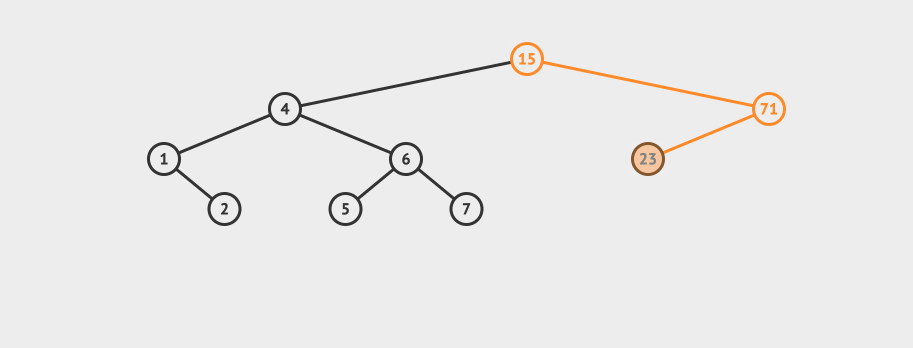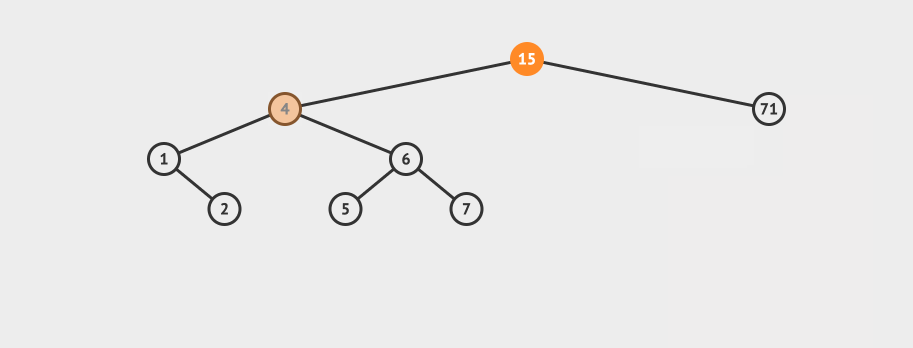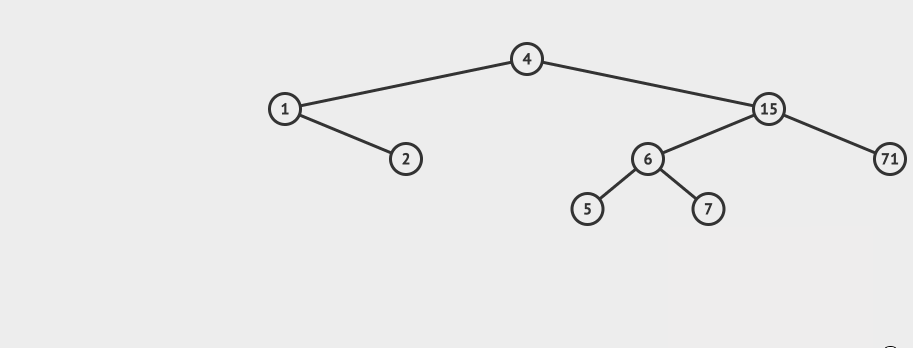
AVL的搜索
AVL的搜索和二叉搜索树的搜索方式是一致的。
先看一个直观的例子，怎么在AVL中搜索到7这个节点：

搜索的基本步骤是：

从根节点15出发，比较根节点和搜索值的大小
如果搜索值小于节点值，那么递归搜索左侧树
如果搜索值大于节点值，那么递归搜索右侧树
如果节点匹配，则直接返回即可。

相应的java代码如下：

//搜索方法，默认从根节点搜索
  public Node search(int data){
    return search(root,data);
  }
  //递归搜索节点
  private Node search(Node node, int data)
  {
    // 如果节点匹配，则返回节点
    if (node==null || node.data==data)
      return node;
    // 节点数据大于要搜索的数据，则继续搜索左边节点
    if (node.data > data)
      return search(node.left, data);
    // 如果节点数据小于要搜素的数据，则继续搜索右边节点
    return search(node.right, data);
  }

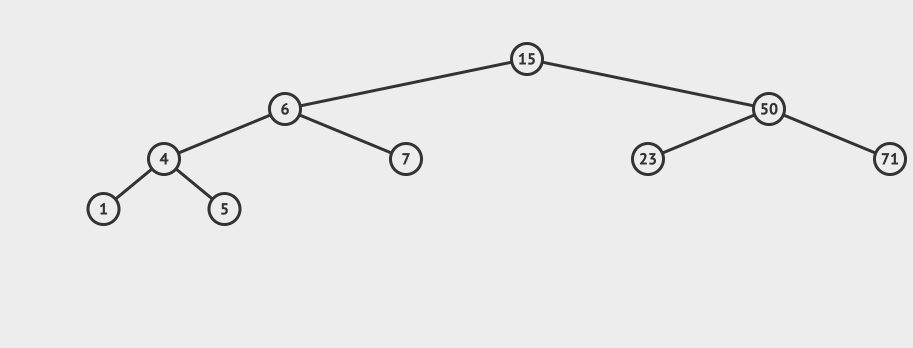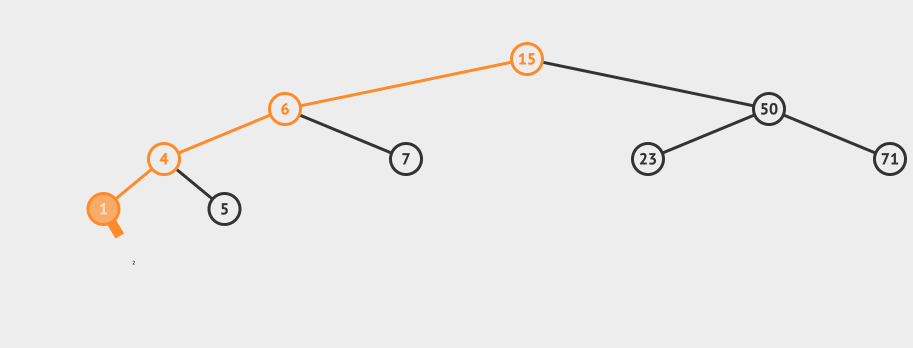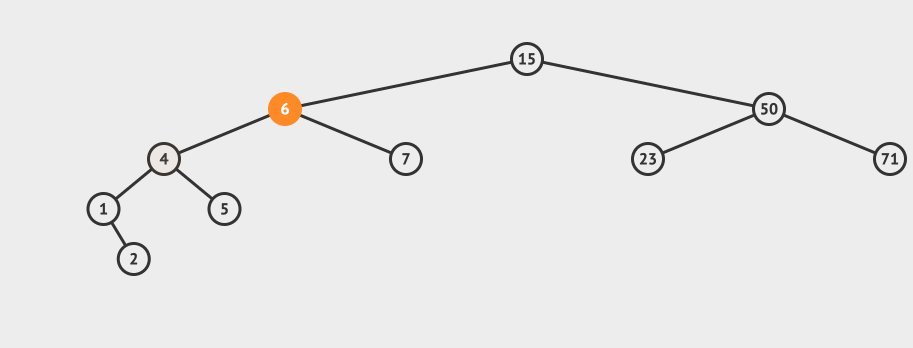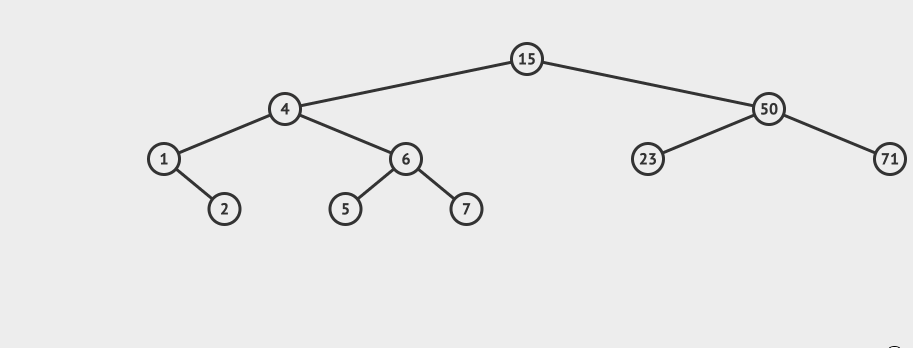
AVL的插入
AVL的插入和BST的插入是一样的，不过插入之后有可能会导致树不再平衡，所以我们需要做一个再平衡的步骤。
看一个直观的动画：

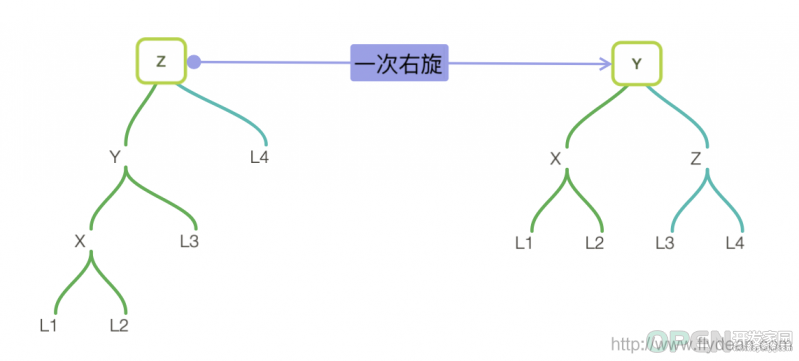
插入的逻辑是这样的：

从根节点出发，比较节点数据和要插入的数据
如果要插入的数据小于节点数据，则递归左子树插入
如果要插入的数据大于节点数据，则递归右子树插入
如果根节点为空，则插入当前数据作为根节点

插入数据之后，我们需要做再平衡。
再平衡的逻辑是这样的：

从插入的节点向上找出第一个未平衡的节点，这个节点我们记为z
对z为根节点的子树进行旋转，得到一个平衡树。

根据以z为根节点的树的不同，我们有四种旋转方式：

left-left：

如果是left left的树，那么进行一次右旋就够了。
右旋的步骤是怎么样的呢？

找到z节点的左节点y
将y作为旋转后的根节点
z作为y的右节点
y的右节点作为z的左节点
更新z的高度

相应的代码如下：

Node rightRotate(Node node) {
    Node x = node.left;
    Node y = x.right;
    // 右旋
    x.right = node;
    node.left = y;
    // 更新node和x的高度
    node.height = max(height(node.left), height(node.right)) + 1;
    x.height = max(height(x.left), height(x.right)) + 1;
    // 返回新的x节点
    return x;
  }

right-right:

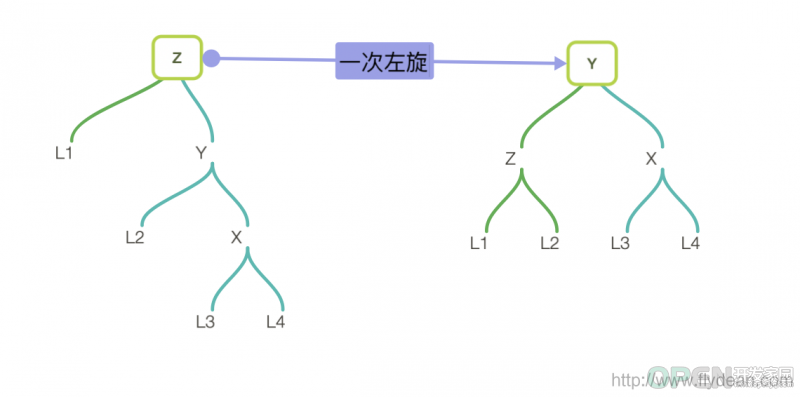
如果是right-right形式的树，需要经过一次左旋：

左旋的步骤正好和右旋的步骤相反：

找到z节点的右节点y
将y作为旋转后的根节点
z作为y的左节点
y的左节点作为z的右节点
更新z的高度

相应的代码如下：

//左旋
  Node leftRotate(Node node) {
    Node x = node.right;
    Node y = x.left;
    //左旋操作
    x.left = node;
    node.right = y;
    // 更新node和x的高度
    node.height = max(height(node.left), height(node.right)) + 1;
    x.height = max(height(x.left), height(x.right)) + 1;
    // 返回新的x节点
    return x;
  }

left-right：

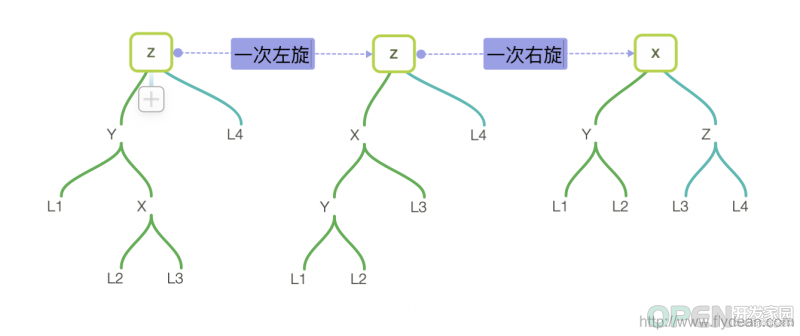
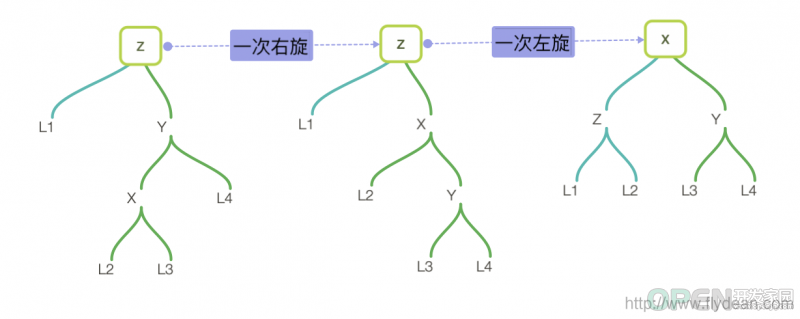
如果是left right的情况，需要先进行一次左旋将树转变成left left格式，然后再进行一次右旋，得到最终结果。

right-left：

如果是right left格式，需要先进行一次右旋，转换成为right right格式，然后再进行一次左旋即可。
现在问题来了，怎么判断一个树到底是哪种格式呢？我们可以通过获取平衡因子和新插入的数据比较来判断：

如果balance>1,那么我们在Left Left或者left Right的情况，这时候我们需要比较新插入的data和node.left.data的大小如果data < node.left.data，表示是left left的情况，只需要一次右旋即可
如果data > node.left.data，表示是left right的情况，则需要将node.left进行一次左旋，然后将node进行一次右旋
如果balance<-1,那么我们在Right Right或者Right Left的情况，这时候我们需要比较新插入的data和node.right.data的大小
如果data > node.right.data，表示是Right Right的情况，只需要一次左旋即可
如果data < node.left.data，表示是Right left的情况，则需要将node.right进行一次右旋，然后将node进行一次左旋

插入节点的最终代码如下：

//插入新节点，从root开始
  public void insert(int data){
    root=insert(root, data);
  }
  //遍历插入新节点
  Node insert(Node node, int data) {
    //先按照普通的BST方法插入节点
    if (node == null)
      return (new Node(data));
    if (data < node.data)
      node.left = insert(node.left, data);
    else if (data > node.data)
      node.right = insert(node.right, data);
    else
      return node;
    //更新节点的高度
    node.height = max(height(node.left), height(node.right)) + 1;
    //判断节点是否平衡
    int balance = getBalance(node);
    //节点不平衡有四种情况
    //1.如果balance>1,那么我们在Left Left或者left Right的情况，这时候我们需要比较新插入的data和node.left.data的大小
    //如果data < node.left.data，表示是left left的情况，只需要一次右旋即可
    //如果data > node.left.data，表示是left right的情况，则需要将node.left进行一次左旋，然后将node进行一次右旋
    //2.如果balance<-1,那么我们在Right Right或者Right Left的情况，这时候我们需要比较新插入的data和node.right.data的大小
    //如果data > node.right.data，表示是Right Right的情况，只需要一次左旋即可
    //如果data < node.left.data，表示是Right left的情况，则需要将node.right进行一次右旋，然后将node进行一次左旋
    //left left
    if (balance > 1 && data < node.left.data)
      return rightRotate(node);
    // Right Right
    if (balance < -1 && data > node.right.data)
      return leftRotate(node);
    // Left Right
    if (balance > 1 && data > node.left.data) {
      node.left = leftRotate(node.left);
      return rightRotate(node);
    }
    // Right Left
    if (balance < -1 && data < node.right.data) {
      node.right = rightRotate(node.right);
      return leftRotate(node);
    }
    //返回插入后的节点
    return node;
  }

AVL的删除
AVL的删除和插入类似。
首先按照普通的BST删除，然后也需要做再平衡。
看一个直观的动画：

删除之后，节点再平衡也有4种情况：

如果balance>1,那么我们在Left Left或者left Right的情况，这时候我们需要比较左节点的平衡因子如果左节点的平衡因子>=0，表示是left left的情况，只需要一次右旋即可
如果左节点的平衡因<0，表示是left right的情况，则需要将node.left进行一次左旋，然后将node进行一次右旋
如果balance<-1,那么我们在Right Right或者Right Left的情况，这时候我们需要比较右节点的平衡因子
如果右节点的平衡因子<=0，表示是Right Right的情况，只需要一次左旋即可
如果右节点的平衡因子>0，表示是Right left的情况，则需要将node.right进行一次右旋，然后将node进行一次左旋

相应的代码如下：

Node delete(Node node, int data)
  {
    //Step 1. 普通BST节点删除
    // 如果节点为空，直接返回
    if (node == null)
      return node;
    // 如果值小于当前节点，那么继续左节点删除
    if (data < node.data)
      node.left = delete(node.left, data);
    //如果值大于当前节点，那么继续右节点删除
    else if (data > node.data)
      node.right = delete(node.right, data);
     //如果值相同，那么就是要删除的节点
    else
    {
      // 如果是单边节点的情况
      if ((node.left == null) || (node.right == null))
      {
        Node temp = null;
        if (temp == node.left)
          temp = node.right;
        else
          temp = node.left;
        //没有子节点的情况
        if (temp == null)
        {
          node = null;
        }
        else // 单边节点的情况
          node = temp;
      }
      else
      {  //非单边节点的情况
        //拿到右侧节点的最小值
        Node temp = minValueNode(node.right);
        //将最小值作为当前的节点值
        node.data = temp.data;
        // 将该值从右侧节点删除
        node.right = delete(node.right, temp.data);
      }
    }
    // 如果节点为空，直接返回
    if (node == null)
      return node;
    // step 2: 更新当前节点的高度
    node.height = max(height(node.left), height(node.right)) + 1;
    // step 3: 获取当前节点的平衡因子
    int balance = getBalance(node);
    // 如果节点不再平衡，那么有4种情况
    //1.如果balance>1,那么我们在Left Left或者left Right的情况，这时候我们需要比较左节点的平衡因子
    //如果左节点的平衡因子>=0，表示是left left的情况，只需要一次右旋即可
    //如果左节点的平衡因<0，表示是left right的情况，则需要将node.left进行一次左旋，然后将node进行一次右旋
    //2.如果balance<-1,那么我们在Right Right或者Right Left的情况，这时候我们需要比较右节点的平衡因子
    //如果右节点的平衡因子<=0，表示是Right Right的情况，只需要一次左旋即可
    //如果右节点的平衡因子>0，表示是Right left的情况，则需要将node.right进行一次右旋，然后将node进行一次左旋
    // Left Left Case
    if (balance > 1 && getBalance(node.left) >= 0)
      return rightRotate(node);
    // Left Right Case
    if (balance > 1 && getBalance(node.left) < 0)
    {
      node.left = leftRotate(node.left);
      return rightRotate(node);
    }
    // Right Right Case
    if (balance < -1 && getBalance(node.right) <= 0)
      return leftRotate(node);
    // Right Left Case
    if (balance < -1 && getBalance(node.right) > 0)
    {
      node.right = rightRotate(node.right);
      return leftRotate(node);
    }
    return node;
  }

本文的代码地址：
learn-algorithm

本文收录于 http://www.flydean.com/11-algorithm-avl-tree/ 
 最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！ 
 欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！

[HarmonyOS] 看动画学算法之:平衡二叉搜索树AVL Tree

相关帖子

为什么输入法不见了打不了中文

电脑自动关机如何解决

电脑自动重启解决方法

pdf怎么搜索内容

电脑没有声音解决方法

itunes打不开修复方法

搜狗高速浏览器搜索记录清除教程

幻灯片会自动跳到下一张解决方法

为什么 DevOps 会失败？

DZ游客搜索提示请求含有非法字符，被系统拒绝的解决方法

飞奔的炮台 LV3

[HarmonyOS] 看动画学算法之:平衡二叉搜索树AVL Tree

相关帖子

为什么输入法不见了 打不了中文

电脑自动关机如何解决

电脑自动重启解决方法

pdf怎么搜索内容

电脑没有声音解决方法

itunes打不开修复方法

搜狗高速浏览器搜索记录清除教程

幻灯片会自动跳到下一张解决方法

为什么 DevOps 会失败？

DZ游客搜索提示请求含有非法字符，被系统拒绝的解决方法

飞奔的炮台 LV3

为什么输入法不见了打不了中文