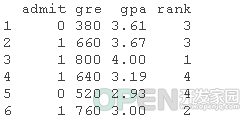
Logistic回归,也称为Logit模型,用于对二元结果变量进行建模。在Logit模型中,结果的对数概率被建模为预测变量的线性组合。例1. 假设我们对影响一个政治候选人是否赢得选举的因素感兴趣。结果(因)变量是二元的(0/1);赢或输。我们感兴趣的预测变量是花在竞选上的钱,花在竞选上的时间,以及候选人是否是现任者。例2. 一个研究者对GRE(研究生入学考试成绩)、GPA(平均分)和本科院校的声望等变量如何影响研究生院的录取感兴趣。因变量,录取/不录取,是一个二元变量。##查看数据的前几行
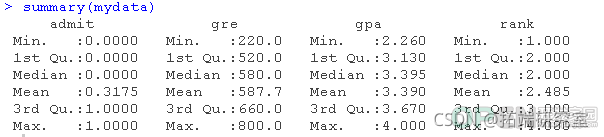
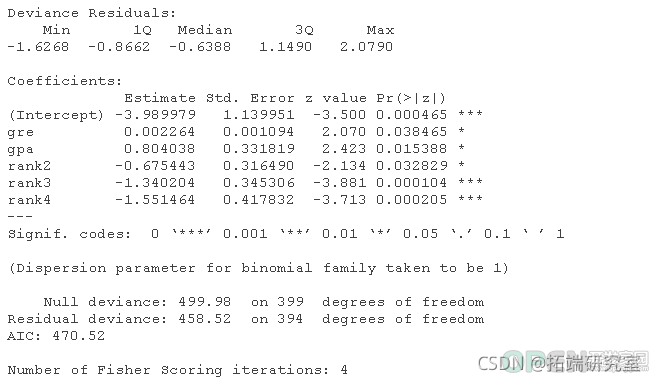
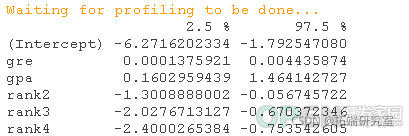
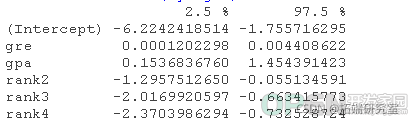
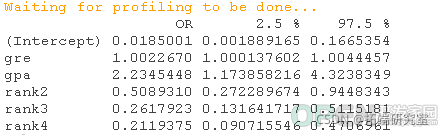
head(mydata)Logistic回归,是本文的重点。 Probit回归。Probit分析会产生类似Logistic回归的结果。选择probit还是logit,主要取决于个人的偏好。 OLS回归。当与二元因变量一起使用时,这个模型被称为线性概率模型,可以作为描述条件概率的一种方式。然而,线性概率模型的误差(即残差)违反了OLS回归的同方差和误差的正态性假设,导致标准误差和假设检验无效。 双组判别函数分析。一种用于二分结果变量的多变量方法。 rank <- factor(rank)在上面的输出中,我们首先看到的是调用,这是R提醒我们所运行的模型是什么,我们指定了哪些选项,等等。 接下来我们看到偏差残差,这是衡量模型拟合度的一个指标。这部分输出显示了模型中使用的各个案例的偏差残差的分布。下面我们讨论如何使用偏差统计的摘要来评估模型的拟合度。 输出的下一部分显示了系数、它们的标准误差、z统计量(有时称为Wald z统计量)以及相关的p值。gre和gpa都有统计学意义,三个等级项也是如此。逻辑回归系数给出了预测变量增加一个单位时结果的对数几率变化。gre每增加一个单位,录取(与未录取)的对数几率增加0.002。 gpa增加一个单位,被研究生院录取的对数几率就会增加0.804。 级别的指标变量有一个稍微不同的解释。例如,就读于排名为2的本科院校与排名为1的院校相比,被录取的对数几率会改变为-0.675。 系数表下面是拟合指数,包括无效和偏差残差以及AIC。稍后我们将展示一个例子,说明如何使用这些值来帮助评估模型的拟合。 wald.test(b , Sigma , L = l)## 概率比
##概率和95%CIdata.frame(mean(gre), mean(gpa), factor(1:4))
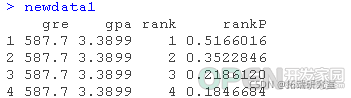
## 查看数据框这些对象的名称必须与上述逻辑回归中的变量相同(例如,在本例中,gre的平均值必须被命名为gre)。 现在我们有了要用来计算预测概率的数据框,我们可以告诉R来创建预测概率。下面的第一行代码非常紧凑,我们将把它拆开来讨论各个部分的作用。newdata1$rankP告诉R,我们要在数据集(数据框)newdata1中创建一个名为rankP的新变量,命令的其余部分告诉R,rankP的值应该是使用predict( )函数进行的预测。括号内的选项告诉R,预测应该基于mylogit分析,预测变量的值来自newdata1,预测的类型是预测的概率(type="response")。代码的第二行列出数据框newdata1中的值。这是预测概率的表格。 predict(mylogit, newdata, type)gre = rep(seq(from = 200, to = 800, length.out = 100),
4), mean(gpa), factor(rep(1:4, each = 100))PredictedProb
LL <- plogis(fit - (1.96 * se.fit))
UL <- plogis(fit + (1.96 * se.fit))
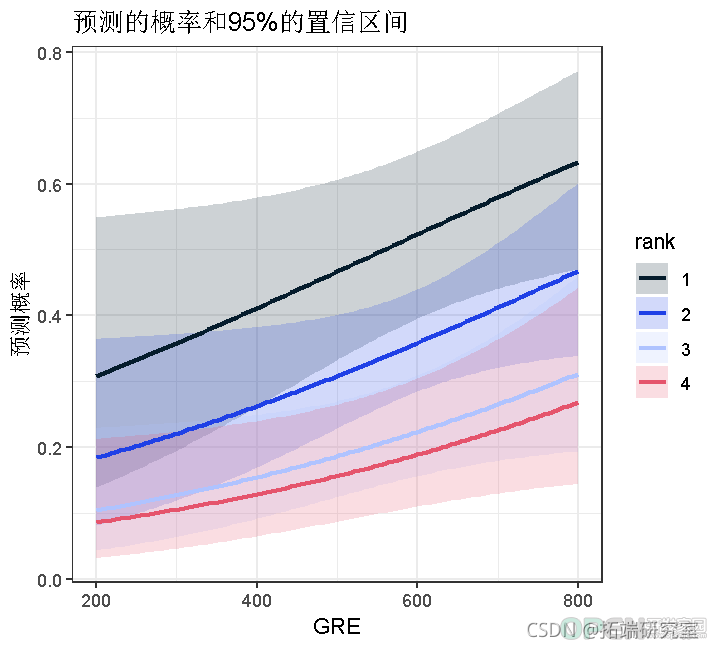
##查看最终数据集的前几行ggplot( aes(x = gre, y = Predicted))with(mylogit, null.deviance - deviance)
## [1] 41.5with(mylogit, df.null - df.residual)
## [1] 5## [1] 7.58e-08logLik(mylogit)
## 'log Lik.' -229 (df=6)需要考虑的事项 空单元格或小单元格。你应该通过分类预测因子和结果变量之间的交叉分析来检查空单元或小单元。如果一个单元的案例很少(小单元),模型可能会变得不稳定或根本无法运行。 样本量。logit和probit模型都需要比OLS回归更多的案例,因为它们使用最大似然估计技术。在只有少量案例的数据集中,有时可以用精确的Logistic回归来估计二元结果的模型。同样重要的是要记住,当结果是罕见的,即使整个数据集很大,也很难估计出一个Logit模型。 伪R平方。存在许多不同的伪R平方的测量方法。它们都试图提供类似于OLS回归中R平方所提供的信息;然而,它们都不能完全按照OLS回归中R平方的解释来解释。 诊断法。逻辑回归的诊断方法与OLS回归的诊断方法不同,对逻辑回归的诊断与对probit回归的诊断相似。 参考文献 
![]() 编程语言
发布于:2021-12-11 10:30
|
阅读数:558
|
评论:0
编程语言
发布于:2021-12-11 10:30
|
阅读数:558
|
评论:0

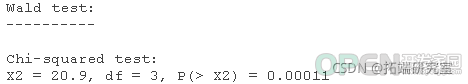
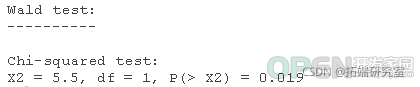



 QQ好友和群
QQ好友和群 QQ空间
QQ空间