不登高山,不知天之高也;不临深溪,不知地之厚也。 ——荀子
这篇文章讲述的是R语言中关于矩阵与数组的相关知识。希望这篇R语言文章对您有所帮助!如果您有想学习的知识或建议,可以给作者留言~
Chapter02 | 矩阵与数组
- 1、创建矩阵
- 2、创建数组
- 3、通过索引访问矩阵
- 4、通过名称访问矩阵
- 5、矩阵的运算
- 6、添加
矩阵是一个按照长方阵列排列的复合或实数集合。向量是一维的,而矩阵是二维的,需要有行和列。
在R软件中,矩阵是有维数的向量,这里的矩阵元素可以是数值型,字符型或者逻辑型,但是每个元素必须都拥有相同的模式,这个和向量是一致的。
R语言中比较出名的矩阵iris3
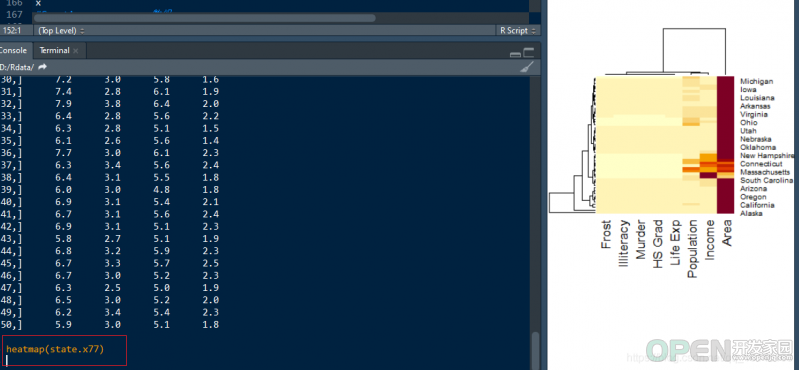
state.x77 # 美国五十个州八个指标
矩阵其实就是给向量加一个维度
1、创建矩阵> x <- 1:20
> x
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
# 定义一个对象m, 用来存储矩阵,第二个参数指定行数,第三个参数用来指定列数,可以省略,直接写4,5
> m <- matrix(x,nrow = 4,ncol = 5)
> m
[,1] [,2] [,3] [,4] [,5]
[1,] 1 5 9 13 17
[2,] 2 6 10 14 18
[3,] 3 7 11 15 19
[4,] 4 8 12 16 20
# 此为上述代码的简写
> m <- matrix(x,4,5)
> m
[,1] [,2] [,3] [,4] [,5]
[1,] 1 5 9 13 17
[2,] 2 6 10 14 18
[3,] 3 7 11 15 19
[4,] 4 8 12 16 20
# 行和列必须要满足条件 4行6列会报错,超过了限制
> m <- matrix(x,nrow = 4,ncol = 6)
Warning message:
In matrix(x, nrow = 4, ncol = 6) :
data length [20] is not a sub-multiple or multiple of the number of columns [6]
#
> matrix(x,4,4)
[,1] [,2] [,3] [,4]
[1,] 1 5 9 13
[2,] 2 6 10 14
[3,] 3 7 11 15
[4,] 4 8 12 16
# 行和列要有一个满足条件,否则会报错 报错原因,因为20不是3的整数倍
> matrix(x,3,3)
[,1] [,2] [,3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
Warning message:
In matrix(x, 3, 3) :
data length [20] is not a sub-multiple or multiple of the number of rows [3]
# 只给一个行或者列会自动分配,矩阵是按照列进行分配的
> matrix(x,4)
[,1] [,2] [,3] [,4] [,5]
[1,] 1 5 9 13 17
[2,] 2 6 10 14 18
[3,] 3 7 11 15 19
[4,] 4 8 12 16 20
# byrow=TURE按行排列,否则按列排列
> m <- matrix(x,nrow = 4,ncol = 5,byrow = TRUE)
> m
[,1] [,2] [,3] [,4] [,5]
[1,] 1 2 3 4 5
[2,] 6 7 8 9 10
[3,] 11 12 13 14 15
[4,] 16 17 18 19 20
# 修改行和列的名称
> rnames <- c("R1","R2","R3","R4")
> cnames <- c("C1","C2","C3","C4","C5")
> dimnames(m)=list (rnames,cnames)
> m
C1 C2 C3 C4 C5
R1 1 2 3 4 5
R2 6 7 8 9 10
R3 11 12 13 14 15
R4 16 17 18 19 20
# dim()函数可以显示向量的维数
> dim(x)
NULL
# 为向量添加函数构建矩阵
> dim(x) <- c(4,5)
> x
[,1] [,2] [,3] [,4] [,5]
[1,] 1 5 9 13 17
[2,] 2 6 10 14 18
[3,] 3 7 11 15 19
[4,] 4 8 12 16 20
2、创建数组# 三维数组,可以理解为一个长宽高分别为2,2,5的矩阵
> dim(x) <- c(2,2,5)
> x
, , 1
[,1] [,2]
[1,] 1 3
[2,] 2 4
, , 2
[,1] [,2]
[1,] 5 7
[2,] 6 8
, , 3
[,1] [,2]
[1,] 9 11
[2,] 10 12
, , 4
[,1] [,2]
[1,] 13 15
[2,] 14 16
, , 5
[,1] [,2]
[1,] 17 19
[2,] 18 20
# Creating an array
> x <- 1:20
> dim(x) <- c(2,2,5)
> dim1 <- c("A1", "A2") # 行
> dim2 <- c("B1", "B2", "B3") # 列
> dim3 <- c("C1", "C2", "C3", "C4") # 给几个值就为几维数组
# dimnames用来定义每个维度的标签
> z <- array(1:24, c(2,3,4), dimnames=list(dim1, dim2, dim3))
> z
, , C1
B1 B2 B3
A1 1 3 5
A2 2 4 6
, , C2
B1 B2 B3
A1 7 9 11
A2 8 10 12
, , C3
B1 B2 B3
A1 13 15 17
A2 14 16 18
, , C4
B1 B2 B3
A1 19 21 23
A2 20 22 24
3、通过索引访问矩阵# 4x5的矩阵m
> m <- matrix(x,nrow = 4,ncol = 5)
> m
[,1] [,2] [,3] [,4] [,5]
[1,] 1 5 9 13 17
[2,] 2 6 10 14 18
[3,] 3 7 11 15 19
[4,] 4 8 12 16 20
# 访问第一行第二列的元素
> m[1,2]
[1] 5
# 访问第一行二,三,四列的元素
> m[1,c(2,3,4)]
[1] 5 9 13
# 访问矩阵一个子集
> m[c(2,4),c(2,3)]
[,1] [,2]
[1,] 6 10
[2,] 8 12
# 访问第二行
> m[2,]
[1] 2 6 10 14 18
# 访问第二列
> m[,2]
[1] 5 6 7 8
# 访问对应的行
> m[2]
[1] 2
# 去除第一行再取第二列
> m[-1,2]
[1] 6 7 8
4、通过名称访问矩阵> dimnames(m)=list (rnames,cnames)
> m
C1 C2 C3 C4 C5
R1 1 5 9 13 17
R2 2 6 10 14 18
R3 3 7 11 15 19
R4 4 8 12 16 20
# 此行出错
> m["C1","C2"]
Error in m["C1", "C2"] : subscript out of bounds
# 通过行名列名访问元素
> m["R1","C2"]
[1] 5
# 出错部分
> m["R1"]
[1] NA
> m["C1"]
[1] NA
> m[,"R1"]
Error in m[, "R1"] : subscript out of bounds
# 想要访问列的名字,访问列
> m["R1",]
C1 C2 C3 C4 C5
1 5 9 13 17
# 想要访问行的名字 ,访问行
> m[,"C1"]
R1 R2 R3 R4
1 2 3 4
5、矩阵的运算此部分为矩阵的一些写法以及计算技巧
实现矩阵的转置,行变列,列变行
> a <- matrix(1:12,nrow = 3,ncol = 4)
> a
[,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12
# 行列互换
> t(a)
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
[4,] 10 11 12
> a <- b <- matrix(1:12,nrow = 3,ncol = 4)
> a+b
[,1] [,2] [,3] [,4]
[1,] 2 8 14 20
[2,] 4 10 16 22
[3,] 6 12 18 24
> a-b
[,1] [,2] [,3] [,4]
[1,] 0 0 0 0
[2,] 0 0 0 0
[3,] 0 0 0 0
> a <- matrix(1:12,nrow = 3,ncol = 4)
> b <- matrix(1:12,nrow = 4,ncol = 3)
> a%*%b 线代矩阵相乘
[,1] [,2] [,3]
[1,] 70 158 246
[2,] 80 184 288
[3,] 90 210 330
求对角线,diag()函数
> a <- matrix(1:16,nrow = 4,ncol = 4)
> a
[,1] [,2] [,3] [,4]
[1,] 1 5 9 13
[2,] 2 6 10 14
[3,] 3 7 11 15
[4,] 4 8 12 16
# 返回对角线
> diag(a)
[1] 1 6 11 16
# 对角线矩阵
> diag(diag(a))
[,1] [,2] [,3] [,4]
[1,] 1 0 0 0
[2,] 0 6 0 0
[3,] 0 0 11 0
[4,] 0 0 0 16
# 产生一个四阶的单位矩阵
> diag(4)
[,1] [,2] [,3] [,4]
[1,] 1 0 0 0
[2,] 0 1 0 0
[3,] 0 0 1 0
[4,] 0 0 0 1
solve()函数
# 先使用rnorm函数随机生成16个随机数,并创建矩阵
> a <- matrix(rnorm(16),4,4)
> a
[,1] [,2] [,3] [,4]
[1,] 0.19496384 -1.32876618 0.8009854 0.1090159
[2,] 0.83996855 -1.31302374 0.4815483 -0.2333306
[3,] -1.71094415 0.03186264 -0.5280415 2.3790375
[4,] -0.03161188 0.85040187 0.4736652 -0.5227957
# solve()函数可以直接求逆
> solve(a)
[,1] [,2] [,3] [,4]
[1,] -2.3313965 3.2960835 0.7418279 1.418528
[2,] -1.1575768 1.2092526 0.4392610 1.217815
[3,] 0.1181362 0.8574405 0.4068229 1.493238
[4,] -1.6349574 2.5445791 1.0382558 1.335292
solve()函数还能解线性方程
eg: ax=b
> a <- matrix(rnorm(16),4,4)
> a
[,1] [,2] [,3] [,4]
[1,] 1.2319870 -0.1801956 0.1470676 0.01413551
[2,] -0.2092927 0.2776381 1.0411766 0.44004831
[3,] 1.3762975 -0.6371769 -1.3026650 -1.20290275
[4,] 0.1149844 0.4075077 0.1193776 -0.21052398
> b <- c(1:4)
> b
[1] 1 2 3 4
> solve(a,b)
[1] 0.894783 3.750849 4.723690 -8.572473
用来求矩阵的特征值与特征向量
> a <- diag(4)+1
> a
[,1] [,2] [,3] [,4]
[1,] 2 1 1 1
[2,] 1 2 1 1
[3,] 1 1 2 1
[4,] 1 1 1 2
> a.e = eigen(a,symmetric = T)
> a.e
eigen() decomposition
$values
[1] 5 1 1 1
$vectors
[,1] [,2] [,3] [,4]
[1,] -0.5 0.8660254 0.0000000 0.0000000
[2,] -0.5 -0.2886751 -0.5773503 -0.5773503
[3,] -0.5 -0.2886751 -0.2113249 0.7886751
[4,] -0.5 -0.2886751 0.7886751 -0.2113249
6、添加colSums(m) # 求矩阵每一列的和
rowSums(m) # 求矩阵每一行的和
colMeans(m) # 求矩阵每一列的平均值
rowMeans(m) # 求矩阵每一行的平均值
n <- matrix (1:9,3,3) # 3行3列的矩阵
t <- matrix (2:10,3,3) # 3行3列的矩阵
n*t # 矩阵的内积
n%*%t # 矩阵的外积
|

![]() 编程语言
发布于:2021-12-27 17:19
|
阅读数:352
|
评论:0
编程语言
发布于:2021-12-27 17:19
|
阅读数:352
|
评论:0

 QQ好友和群
QQ好友和群 QQ空间
QQ空间