Android 音频可视化，阿里巴巴开发手册2021

小蚂蚁

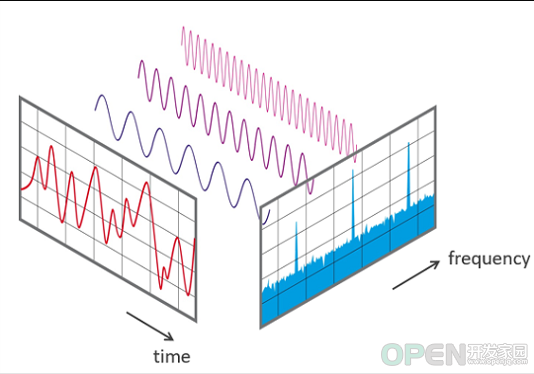
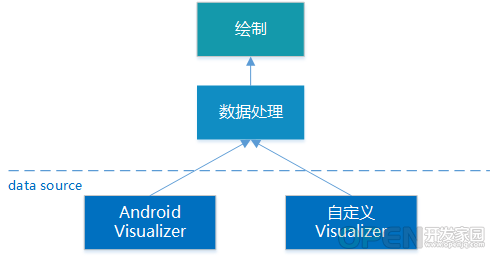
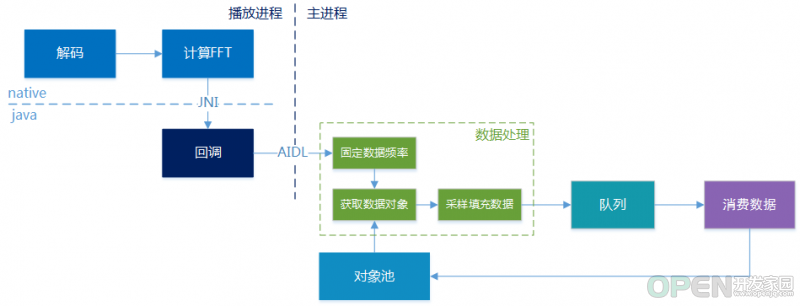
播放器从本地音频文件或网络加载编码后的音频数据，解码为 pcm 数据写入 AudioTrack
AudioTrack 将 pcm 数据写入 FIFO
AudioFlinger 中的 MixerThread 通过 AudioMixer 读取 FIFO 中的数据进行混音后写入 HAL 输出设备进行播放

在这个流程中，直接体现音频特征，可用于可视化绘制的是 pcm 数据。但 pcm 表示各采样时间点上音频信号强度，看起来杂乱无章，难以体现听觉感知到的声音变化。pcm 数据仅可用来绘制体现音频信号平均强度变化的可视化动效，其他大部分动效需要使用对 pcm 数据做傅里叶变换后得到的体现各频率点上信号强度变化的频域数据来绘制。
这里简单回顾下傅里叶变换，它将信号从时域转换为频域，一般用于信号频谱分析，确定其成分。转换结果如下图所示：

pcm 数据是时间离散的，需要使用离散傅里叶变换（DFT），它将包含 N 个复数的序列 {xn}:\=x0,x1,...,xN?1\{x_n\}:=x_0, x_1, ..., x_{N-1}{xn?}:\=x0?,x1?,...,xN?1? 转换为另一个复数序列 {Xk}:\=X0,X1,...,XN?1\{X_k\}:=X_0, X_1, ..., X_{N-1}{Xk?}:\=X0?,X1?,...,XN?1?，计算公式为：
Xk\=∑n\=0N?1xn?e?i2πknN\=∑n\=0N?1xn?(cos(2πknN)?i?sin(2πknN))X_k=\sum_{n=0}^{N-1}x_n \cdot e^{-i2 \pi {kn \over N}}=\sum_{n=0}^{N-1}x_n \cdot (cos(2\pi {kn \over N})-i \cdot sin(2\pi {kn \over N}))Xk?\=n\=0∑N?1?xn??e?i2πNkn?\=n\=0∑N?1?xn??(cos(2πNkn?)?i?sin(2πNkn?))
直接用上面公式计算长度为 N 的序列的 DFT，时间复杂度为 O(N2)O(N^2)O(N2)，速度较慢，实际应用中，一般会使用快速傅里叶变换（FFT），将时间复杂度降为 O(Nlog(N))O(Nlog(N))O(Nlog(N))。
计算公式看起来很复杂，但不懂也不会影响我们实现音频可视化，FFT 的计算可以使用已有的库，不需要自己来实现。但为了从 FFT 的计算结果得到最终用来绘制的数据，有必要了解以下DFT特性：

输入全部为实数时，输出结果满足共轭对称性：XN?k\=Xk?X_{N-k}=X_k^*XN?k?\=Xk??，因此一般实现只返回一半结果
如原始信号采样率为 fsf_sfs?，序列长度为 N，输出频率分辨率为 fs/Nf_s/Nfs?/N，第 k 个点的频率为 kfs/Nkf_s/Nkfs?/N，可用于查找指定频率范围在结果中对应的位置
如一个频率对应输出的实部和虚部为 re 和 im，其模为 M\=re2+im2M=\sqrt{re^2+im^2}M\=re2+im2?，原始信号振幅为 A\={M/NDC2M/NotherA=\begin{cases} M/N & DC \\ 2M/N & other \end{cases}A\={M/N2M/N?DCother?，可用于计算分贝和数据缩放

数据源
提供播放 pcm 数据的 FFT 计算结果的数据源有两种，一种是 Android 系统提供的 Visualizer 类，这种存在兼容性问题，因此我们引入了另一种自己实现的数据源。同时，我们实现了在不修改上层各动效的数据处理和绘制逻辑的基础上切换数据源，如下图所示：

Android Visualizer
系统 Visualizer 提供了方便的 api 来获取播放音频的波形或 FFT 数据，一般使用方式是：

用 audio session ID 创建 Visualizer对象，传 0 可获取混音后的可视化数据，传特定播放器或 AudioTrack 所使用的 audio session 的 ID，可获取它们所播放音频的可视化数据
调 setCaptureSize 方法设置每次获取的数据大小，调 setDataCaptureListener 方法设置数据回调并指定获取数据频率（即回调频率）和数据类型（波形或 FFT）
调 setEnabled 方法开始获取数据，不再需要时调 release 方法释放资源

更详细的 api 信息可查看[官方文档]( )。
系统 Visualizer 输出的数据大小正比于音量，当音量为 0 时，输出也为 0，可视化效果会随音量变化。
使用系统 Visualizer 存在兼容性问题，在有些机型上会导致系统音效失效，如要在所有机型上都能无副作用地展示动效，需要实现自定义 Visualizer。
自定义 Visualizer
作为跟系统 Visualizer 功能一致的数据源，自定义 Visualizer 需具备两个功能：

获取 pcm 数据，计算 FFT
以指定频率和大小发送 FFT 数据

实现第一个功能首先要获取播放音频的 pcm 数据，这要求使用的播放器能够提供 pcm 数据，我们的播放器是自己实现的，能够满足这个要求。我们对播放器进行了扩展，增加了收集解码后的 pcm 数据计算 FFT 的功能。
由于不同音频采样率不同，而计算 FFT 时采用固定的窗口大小，导致 FFT 计算结果回调频率随播放音频改变，同时指定的数据大小可能跟计算结果的大小不同，因此要实现第二个功能，需要对计算结果做固定频率和采样等处理。
另外，我们的播放器在播放进程中运行，而实际使用 FFT 数据的动效页面运行于主进程中，所以还需要跨进程传输数据。
综上，自定义 Visualizer 的整体流程是：在播放进程 native 层中计算 FFT，通过 JNI 调用，把计算结果回调给Java 层，然后通过 AIDL 把 FFT 数据传递给主进程进行后续的数据处理和发送操作。如下图所示：

固定频率需要将可变的 FFT 计算结果回调频率转换为外部设置的 Visualizer 回调频率，如下图所示：

根据所需数据发送时间间隔和 FFT 回调时间间隔差值的不同，我们采用两种不同的方式。
当时间间隔差值小于等于回调时间间隔时，每 t/Δtt/ \Delta tt/Δt 次回调丢弃一次数据，其中 t 为 FFT 回调时间间隔，Δt\Delta tΔt 为时间间隔差值，如下图所示：

当时间间隔差值大于回调时间间隔时，每 t1/tt1/tt1/t 次回调发送一次数据，其中 t1 为所需数据发送时间间隔，t 为 FFT 回调时间间隔，如下图所示：

采样就是当外部设置的数据大小小于 FFT 计算结果的数据大小时，对原始 FFT 数据以合适的间隔抽取数据，以满足设置的要求。
为了让自定义 Visualizer 返回数据的取值范围跟系统 Visualizer 一致，从而实现数据源无缝切换，我们需要对 FFT 数据进行缩放。这里就需要用到前面提到的模与振幅的计算了，解码所得 pcm 数据的取值范围为 [-1, 1]，所以原始信号振幅取值范围为 [0, 1]，即 2M/N2M/N2M/N 的取值范围为 [0, 1]（绘制时不会用到直流分量，这里不考虑）；而系统 Visualizer 返回的 FFT 数据是一个 byte 数组，实部和虚部的取值范围为 [-128, 128]，模的取值范围为 [0,128×2][0, 128 \times \sqrt2][0,128×2?]，那么 2M/N×128×22M/N \times 128 \times \sqrt22M/N×128×2? 的取值范围跟系统 Visualizer 输出 FFT 的模的取值范围一致。由于绘制不会用到相位信息，我们可以将用上述方式缩放后的值作为输出 FFT 数据的实部，并把虚部设为 0。
由于数据发送的频率较高，为了避免频繁创建对象导致内存抖动，我们采用对象池来保存数据数组对象，每次从对象池中获取所需大小的数组对象，填充采样数据后加入到队列中等待发送，数据消费完后将数组对象返回到对象池中。

数据处理
不同动效的具体数据处理方式不同，忽略细节上的差异，云音乐现有的动效中，除了宇宙尘埃和孤独星球，其他的处理流程基本一致，如下图所示：

首先根据动效选择的频率范围计算所需的频率数据在 FFT 数组中的索引位置：
fr\=fs/N,start\=?MIN/fr?,end\=?MAX/fr?f_r=f_s/N, start=\lceil MIN/f_r \rceil, end=\lfloor MAX/f_r \rfloorfr?\=fs?/N,start\=?MIN/fr??,end\=?MAX/fr??
其中 fsf_sfs? 为采样率，N 为 FFT 窗口大小，frf_rfr? 为频率分辨率，MIN 为频率范围起始值，MAX 为频率范围结束值。
然后根据动效所需数据点数，对频率范围内的 FFT 数据进行采样或用一个 FFT 数据表示多个数据点。
然后计算分贝：
db\=20log?10Mdb=20\log_{10}Mdb\=20log10?M
其中 M 为 FFT 数据的模。
然后将分贝转化为高度：
h\=db/MAX_DB?maxHeighth=db/MAX\_DB \cdot maxHeighth\=db/MAX_DB?maxHeight

学习分享
在当下这个信息共享的时代，很多资源都可以在网络上找到，只取决于你愿不愿意找或是找的方法对不对了
很多朋友不是没有资料，大多都是有几十上百个G，但是杂乱无章，不知道怎么看从哪看起，甚至是看后就忘
如果大家觉得自己在网上找的资料非常杂乱、不成体系的话，我也分享一套给大家，比较系统，我平常自己也会经常研读。
2020最新上万页的大厂面试真题

七大模块学习资料：如NDK模块开发、Android框架体系架构...

只有系统，有方向的学习，才能在段时间内迅速提高自己的技术。

这份体系学习笔记，适应人群：
第一，学习知识比较碎片化，没有合理的学习路线与进阶方向。
第二，开发几年，不知道如何进阶更进一步，比较迷茫。
第三，到了合适的年纪，后续不知道该如何发展，转型管理，还是加强技术研究。如果你有需要，我这里恰好有为什么，不来领取！说不定能改变你现在的状态呢！
由于文章内容比较多，篇幅不允许，部分未展示内容以截图方式展示。如有需要获取完整的资料文档的朋友点击我的GitHub免费获取。

[PHP] Android 音频可视化，阿里巴巴开发手册2021

相关帖子

浏览过的版块

Android实现两台手机屏幕共享和远程控制

国内首发可视化智能调优平台，小龙带你玩转KeenTune UI

Android实现实时视频聊天功能｜源码 Demo 分享

Android自定义View学习（1）——基础知识介绍

Android 知识体系

Android 自定义圆形取色盘

知识星球的音频怎么下载？知识星球音频下载到电脑图文教程

笔记本未安装音频设备解决方法

电脑如何安装音频设备

Android控件Spinner实现下拉列表及监听功能

小蚂蚁 LV3