|
|
编辑距离(Edit Distance)
我们在日常搜索中会出现一些错误,这些错误主要分为两种:一种是拼写错误,出现一些错别字,另外一些就是词是对的,但是不符合特定的场合。具体案例如下:
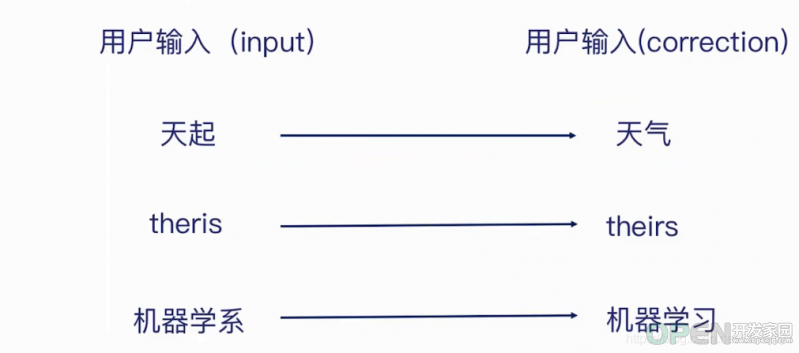
在这里我们先介绍一种计算错误拼写的方式——编辑距离(edit distance),编辑距离,又称Levenshtein距离是指两个字串之间,由一个转成另一个所需的最少编辑操作次数,如果它们的距离越大,说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。这个概念是由俄罗斯科学家Vladimir Levenshtein在1965年提出来的,所以也叫 Levenshtein 距离。它可以用来做DNA分析,拼字检测,抄袭识别等等。总是比较相似的,或多或少我们可以考虑编辑距离。在编辑距离中,主要包括用户输入(users input)、候选(candidate)以及编辑距离的计算。在编辑距离计算过程中,我们通常用到了三种最主要的操作:插入(insert)、删除(delete)、替换(replace),具体计算流程如下:
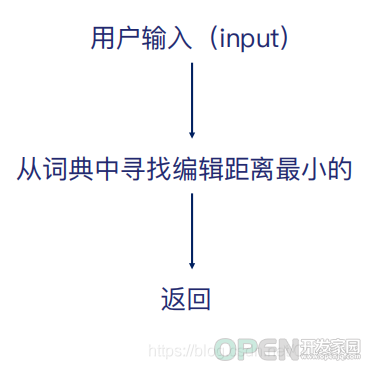
例如我们要计算如下的编辑距离:
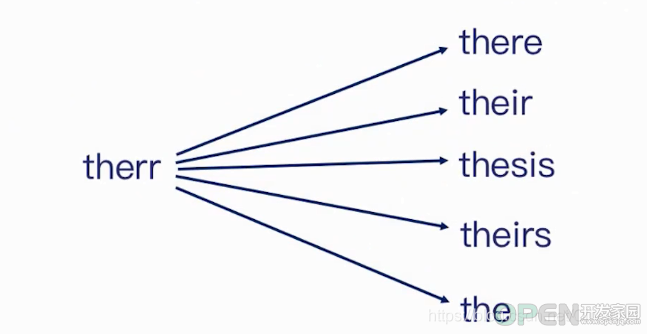
对应计算的编辑距离为:

具体的算法过程如下:
1、str1或str2的长度为0返回另一个字符串的长度。 if(str1.length0) return str2.length; if(str2.length0) return str1.length;
2、初始化(n+1)(m+1)的矩阵d,并让第一行和列的值从0开始增长。扫描两字符串(nm级的),如果:str1 == str2[j],用temp记录它,为0。否则temp记为1。然后在矩阵d[i,j]赋于d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp三者的最小值。
3、扫描完后,返回矩阵的最后一个值d[n][m]即是它们的距离。
我们紧接着还要其相似度,计算公式为1-它们的距离/两个字符串长度的最大值。接下来我们实现这个计算过程。首先我们先创建一个矩阵,或者说是我们的二维数列,假设有两个字符串,我们的字符串的长度分别是m和n,那么,我们矩阵的维度就应该是(m+1)*(n+1)。不过这里需要我们注意的是我们先给数列的第一行第一列赋值,从0开始递增赋值,之后我们计算第一列,第二列,依次类推,算完整个矩阵。我们的计算规则为:d[i,j]=min(d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp) 这三个当中的最小值。其中:str1 == str2[j],用temp记录它,为0。否则temp记为1。我们用d[i-1,j]+1表示增加操作,d[i,j-1]+1 表示我们的删除操作,d[i-1,j-1]+temp表示我们的替换操作。并且我们举证元素的产生 Matrix[i - 1, j] + 1 ; Matrix[i, j - 1] + 1 ; Matrix[i - 1, j - 1] + t 三者当中的最小值。最后就依次类推直到矩阵全部生成。接下来我们以therr与thresis为例,用python将其实现。def minEditDist(sm, sn):
m, n = len(sm) + 1, len(sn) + 1
matrix = [[0] * n for i in range(m)]
matrix[0][0] = 0
for i in range(1, m):
matrix[i][0] = matrix[i - 1][0] + 1
for j in range(1, n):
matrix[0][j] = matrix[0][j - 1] + 1
for i in range(m):
print(matrix[i])
print ("********************")
cost = 0
for i in range(1, m):
for j in range(1, n):
if sm[i - 1] == sn[j - 1]:
cost = 0
else:
cost = 1
matrix[i][j] = min(matrix[i - 1][j] + 1, matrix[i][j - 1] + 1, matrix[i - 1][j - 1] + cost)
for i in range(m):
print(matrix[i])
return matrix[m - 1][n - 1]
mindist = minEditDist("therr", "thesis")
print (mindist)
其形成矩阵以及编辑距离如下图所示:
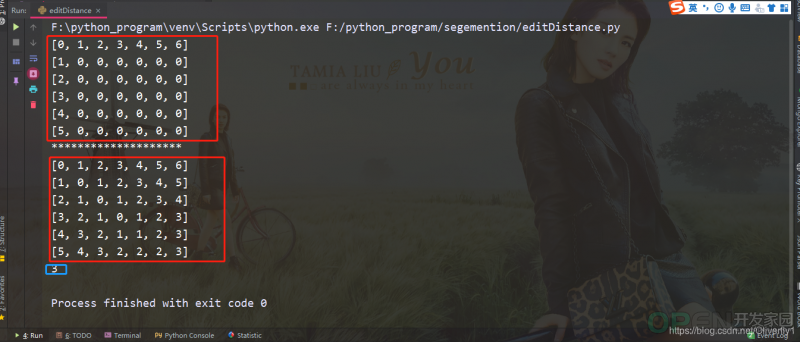
最后得到的结果,距离就是最后右下角的那个值3。接下来我们计算其相似度,根据我们之前提到的,similar = 1 - 1/Math.max(“therr”.length, “thesis”.length)=0.83。根据以上的代码以及计算过程可知,该算法的时间复杂度与词库相关,大致是O(n)。这里是我们基于动态规划实现的。不过我们可以优化该编辑距离的过程,将其复杂度降低,我们现在优化后的流程图如图所示:
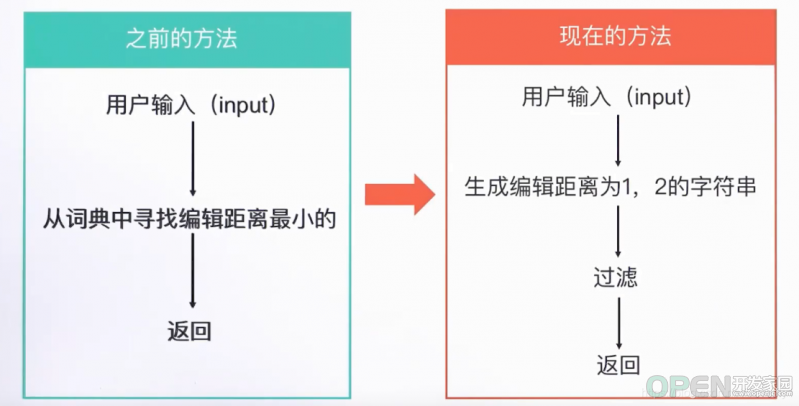
由此可以,我们从原来的从词典中寻找编辑距离最小的改为直接生成编辑距离大致为1~2的字符串,并且还添加了过滤层,将最好的结果返回给用户。例如:
假如用户输入“”appl”
如果我们用add操作产生的编辑距离为1的结果有:appll、bappl、abppl、acppl……
如果我们用replace操作产生编辑距离为1的结果有:bppl、cppl、aapl、abpl……
如果我们用delete操作产生编辑距离为1的结果有:ppl、apl、app……
由上面的案例可知我们在生成的过程中会产生很多词库,因此我们必须要进行过滤。那么我们应该用什么方式进行过滤呢?接下来我们给出一个问题定义,具体定义如下:
给出一个字符串S,我们要找出最有可能修改后的字符串C,并且C∈[w1,w2,……,wn]。也就是有关系式:

我们可以进一步化解该关系式,过程如下:

在这里,p(s|c)中,其中的s是指:用户输入的数据,c是指用户输入正确的数据。因此p(s|c)的含义为:对于一个正确的字符串,有多大的概率确保是s的形式,所以这里的p(c|s)从历史的数据中即可得知。而p©可以通过独立分布将其求出。
动态规划(Dymic Program)
动态规划是我们NLP学习中最核心的算法之一,前篇文章我们大概介绍了动态规划与贪心算法的区别,现在我们详细给大家介绍动态规划的相关知识。首选i让我们在维基百科中看动态规划的定义:动态规划(英语:Dynamic programming,简称DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。说的通俗点就是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
基本思想为:由于动态规划解决的问题多数有重叠子问题这个特点,为减少重复计算,对每一个子问题只解一次,将其不同阶段的不同状态保存在一个二维数组中。也就是说:首先是拆分问题,我的理解就是根据问题的可能性把问题划分成一步一步这样就可以通过递推或者递归来实现.关键就是这个步骤,动态规划有一类问题就是从后往前推到,有时候我们很容易知道:如果只有一种情况时,最佳的选择应该怎么做.然后根据这个最佳选择往前一步推导,得到前一步的最佳选择。然后就是定义问题状态和状态之间的关系,我的理解是前面拆分的步骤之间的关系,用一种量化的形式表现出来,类似于高中学的推导公式,因为这种式子很容易用程序写出来,也可以说对程序比较亲和(也就是最后所说的状态转移方程式),我们再来看定义的下面的两段,我的理解是比如我们找到最优解,我们应该讲最优解保存下来,为了往前推导时能够使用前一步的最优解,在这个过程中难免有一些相比于最优解差的解,此时我们应该放弃,只保存最优解,这样我们每一次都把最优解保存了下来,大大降低了时间复杂度。
首先递归应该是我们解决动态规划问题最常用的方法,帅,速度不算太慢,那么递归到动规的一般转化方法为:如果该递归函数有n个参数,那么就定义一个n维数组,数组下标是递归函数参数的取值范围(也就是数组每一维的大小).数组元素的值就是递归函数的返回值(初始化为一个标志值,表明还未被填充),这样就可以从边界值开始逐步的填充数组,相当于计算递归函数的逆过程(这和前面所说的推导过程应该是相同的)。具体实现如下:
1、将原问题分解为子问题(开头已经介绍了怎么分解) (注意:1,子问题与原问题形式相同或类似,只是问题规模变小了,从而变简单了; 2,子问题一旦求出就要保存下来,保证每个子问题只求解一遍)
2、确定状态(状态:在动规解题中,我们将和子问题相关的各个变量的一组取值,称之为一个"状态",一个状态对应一个或多个子问题所谓的在某个状态的值,这个就是状态所对应的子问题的解,所有状态的集合称为"状态空间".我的理解就是状态就是某个问题某组变量,状态空间就是该问题的所有组变量) 另外:整个问题的时间复杂度就是状态数目乘以每个状态所需要的时间
3、确定一些初始状态(边界条件)的值 (这个视情况而定,千万别以为就是最简单的那个子问题解,上面只是例子,真正实践动规千变万化)
4、确定状态转移方程 (这一步和第三步是最关键的 记住"人人为我"递推,由已知推未知)
总结
我们今天是介绍了文本处理流程中的拼写纠错,详细介绍了编辑距离,从原理到实现,还将其改进版进行了简单的介绍和推导,在文章的最后给大家详细介绍了本文中最为中的算法——动态规划,该部分均是摘自BS有前途的内容,如果本文看不清楚,还可以去看他的这篇博客,写的挺好。接下来给大家介绍过滤词、停顿词的相关知识。
参考文献
[1] 动态规划
[2] 编辑距离算法
|
免责声明:
1. 本站所有资源来自网络搜集或用户上传,仅作为参考不担保其准确性!
2. 本站内容仅供学习和交流使用,版权归原作者所有!© 查看更多
3. 如有内容侵害到您,请联系我们尽快删除,邮箱:kf@codeae.com
|

![]() 开发技术
发布于:2021-07-06 11:24
|
阅读数:538
|
评论:0
开发技术
发布于:2021-07-06 11:24
|
阅读数:538
|
评论:0









 QQ好友和群
QQ好友和群 QQ空间
QQ空间