决策树
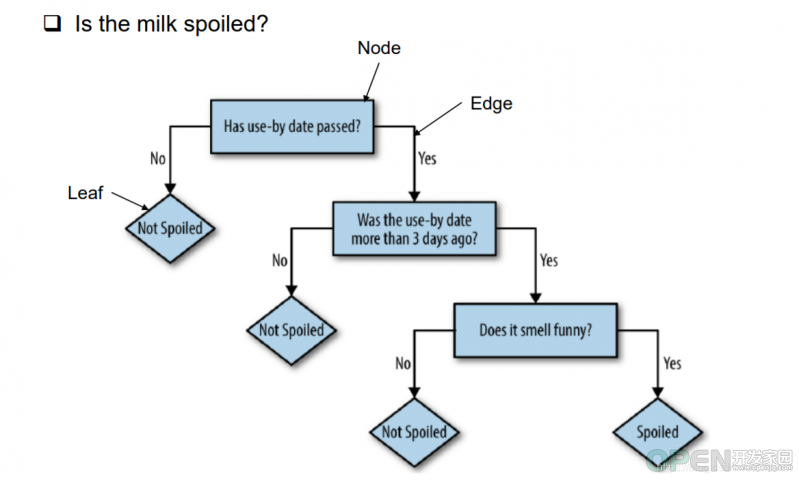
我们喝牛奶时的思考过程就是决策树的一种,通过不同的条件分支生成不断的结果,而结果又有新的条件分支生成新的结果……
上面的例子是:
没过期
没超过三天
新鲜
不新鲜
已经买了放在冰箱里的牛奶
确认保质期
过期与否
过期了几天
喝
过期超过三天
喝
喝
丢了
鲜牛奶的贮藏过程中得益于现在的贮藏技术越来越好,一般稍有过期的产品价格低且仍让可使用,而保质期是指的最佳食用期而不是过了这个期限就不可食用了。因此,对于喝牛奶这个行为,用决策树来表达自己影响自己做出决定的方式就如上图展现了。
在这个决策树种,根部的选择不是随机的,根部往往是对决策产生最核心影响的原因,而其他的叶部分均为根的派生。在使用决策树进行预测森林覆盖时,我们需要考虑的条件有很多,如光照、土质、风力等;诸多的元素会对决策造成影响,而我们的目标就是通过决策树创建一个合理的模型,能够令其预测出因素变化产生的结果。在这个过程中,我们面临一个问题,到底哪一个因素才是最重要的?才是决策树的根部,对于我们一般思考而言,只能说树的栽培光照突然风力雨露等因素都是重要的,却无法真正意义上区分出哪一个更重要,而我们又需要决策树来生成并帮助我们预测结果,这个过程就是我们接下来探讨的过程。
例子
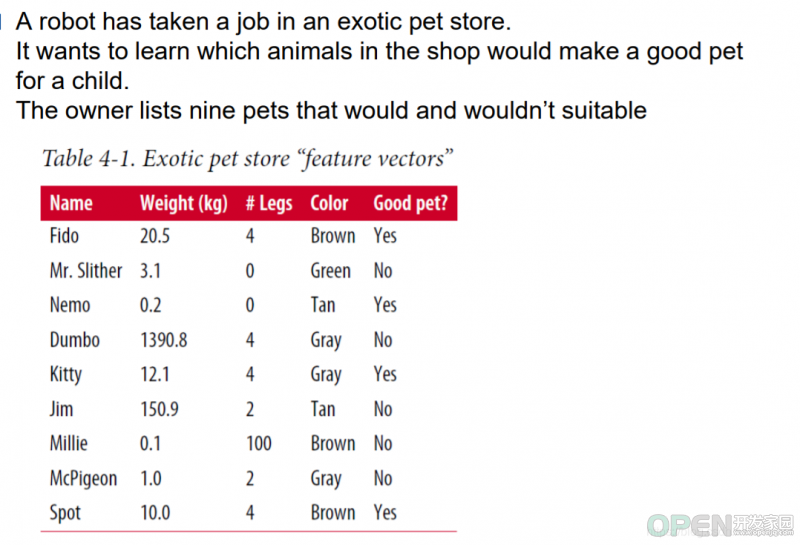
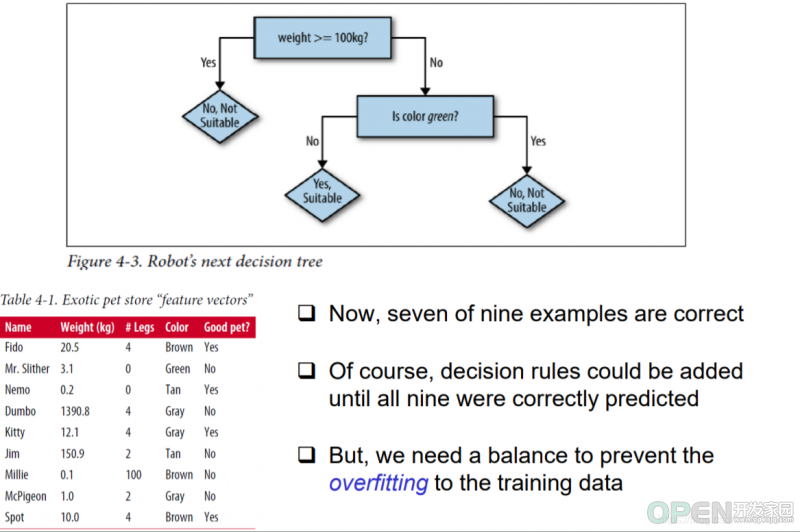
为客人推荐宠物的机器人工作。它需要根据我们给定的资料来模拟,确定出决策树判断的优先条件,这里的条件有体重,腿数目,颜色三要素。
上图反映的判断一个动物是否适合做宠物:
- 体重大于100kg与否,大于则不适合
- 若体重小于100Kg,是否是绿色,绿色则不适合
这样的简单模型对上面的数据进行过滤可以得到一个不太准确的结果,会出现2个判断错误的例子。我们可以通过在是绿色后面再追加一个新的判断语句,根据腿数判断来将这个训练数据的预测值达到100%准确。但是:
当我们创建一个简单的模型时,会发现几个问题:模型的指定会出现一些对训练数据不准确反映的现象,但是如果我们针对这种现象去丰满模型,就可能出现过拟合,导致对普适性差,泛性差的情况。因此我们需要去找到一个平衡点,来找到普适性模型。
2.今天要不要去打高尔夫
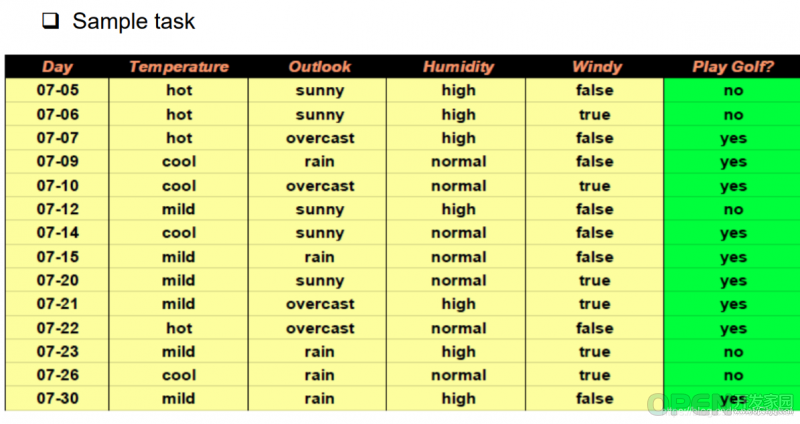
对应的生成树:
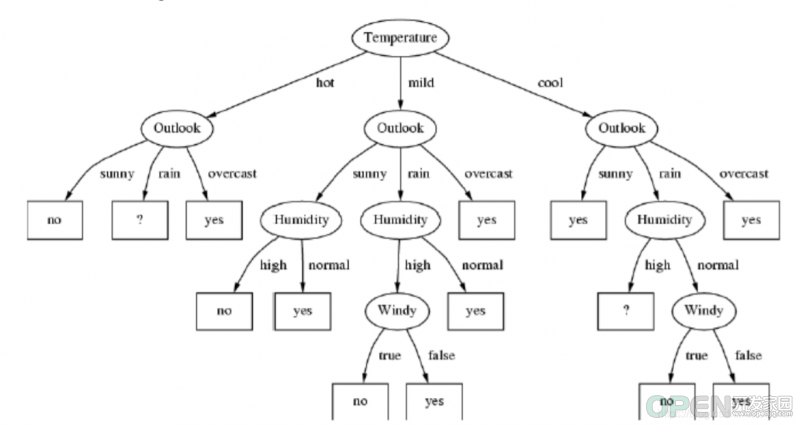
这个决策树的普适性很高,我们可以借此来总结一下决策树。

一个好的决策树对于每个事件的判断,我们希望能够尽可能简介,所有的后续判断尽可能只发生在一侧。举个例子,像起初的牛奶例子,每个判断完成后,都有一个简洁的终结选项——喝;而对应的其他多种多样的判断条件也没有过多的展开。然而实际上决策树的判断更多的是上图中的例子,相对复杂且每一个节点都可能有多个分支,分支中还有分支,整个算法的复杂度就会大大提升。该算法最简单的情况下复杂度是0,一条从头到尾的直线框图;最复杂的情况是log函数,因为每个节点不一定有几个分支,所以无法确认底数。
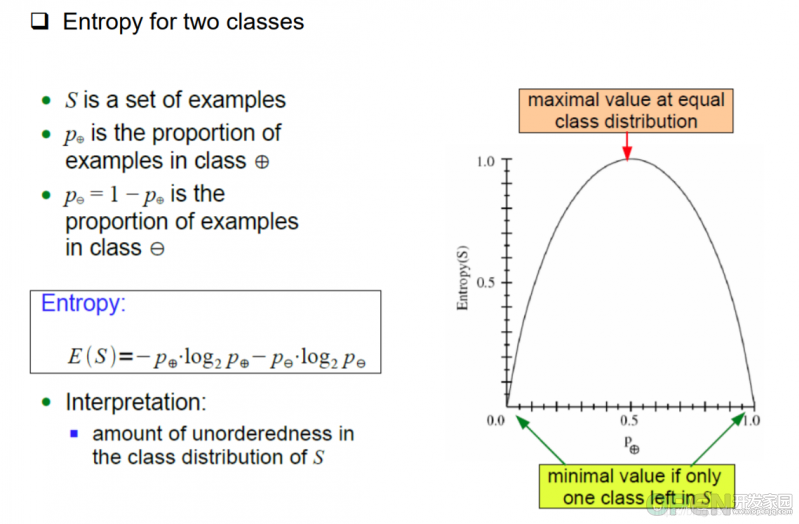
进而我们引出一个概念——Entropy(熵)。如上图所示,是两类数据类型的图形,当二者之一为0是,熵也为0,;当二者55开始,熵值最高,也就说复杂度最高。就反映了我们刚才说的,如果树的分支只偏向一个方向,那么其实树就是一个N节点的线段,复杂度为0,否则复杂度是nlongn。
而对于公式的计算,如下图所示:

需要注意的是在这个计算过程中,0log0视为0而不是负无穷。因为当某一个选项没出现时,它的出现率就是0而不是无穷。
分析以上式子的结构,对于outlook这一个因素,有三个分支,分别是overcast,sunny,rainy。然后统计第一个图中对应的yes/no个数,并根据其个数计算系数。如表格Outlook中对应的overcast出现了4个yes,0个no。其中,yes占据4/4也就是1,而no占据0/4也就是0。其他的也同理, ( 占 据 的 份 数 / 总 数 ) ∗ l o g ∗ ( 占 据 的 份 数 / 总 数 ) (占据的份数/总数)*log*(占据的份数/总数) (占据的份数/总数)∗log∗(占据的份数/总数)就是对应的计算方式。
如果我们只想要计算出具体因素中的某一个具体的项,则需要来看下一个公式。

计算由分割产生的所有集合的加权平均值即可。
信息增益

有了基本概念后,我们来看信息增益。
- 选择差异(信息增益)最大化的属性
- 最大化信息增益等于最小化平均熵
- 当属性A将集合S分割为子集Si时,我们计算平均熵。然后比较原始集合S的和与熵
原始集合S的熵计算:
(结果所占总体的分数/结果总数)log(结果所占总体的分数/结果总数)
对于这例子的原集合熵S= − ( 9 14 l o g ( 9 14 ) + 5 14 l o g ( 5 14 ) ) -(\frac{9}{14}log(\frac{9}{14})+\frac{5}{14}log(\frac{5}{14})) −(149log(149)+145log(145))
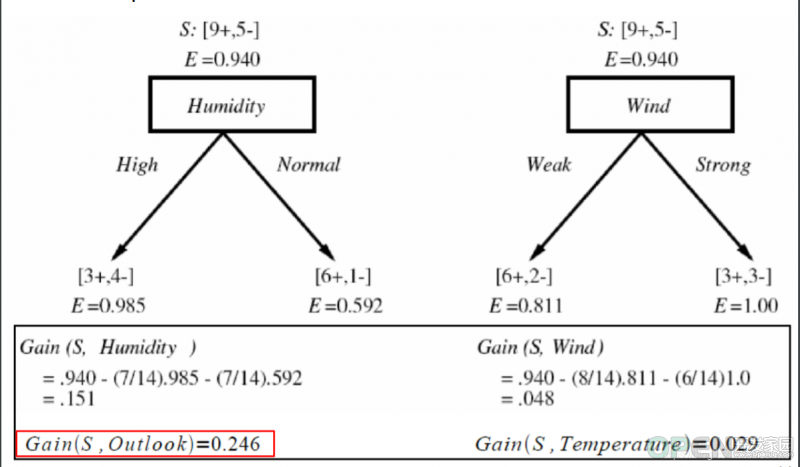
套公式比较出两个因素影响的最大值。值大的一方说明比另一个因素在训练数据上从统计意义上表现出更加重要的判断要素。换言之,值高的相对成为上位节点,最上位节点也就说根一定是信息增益值最大的。
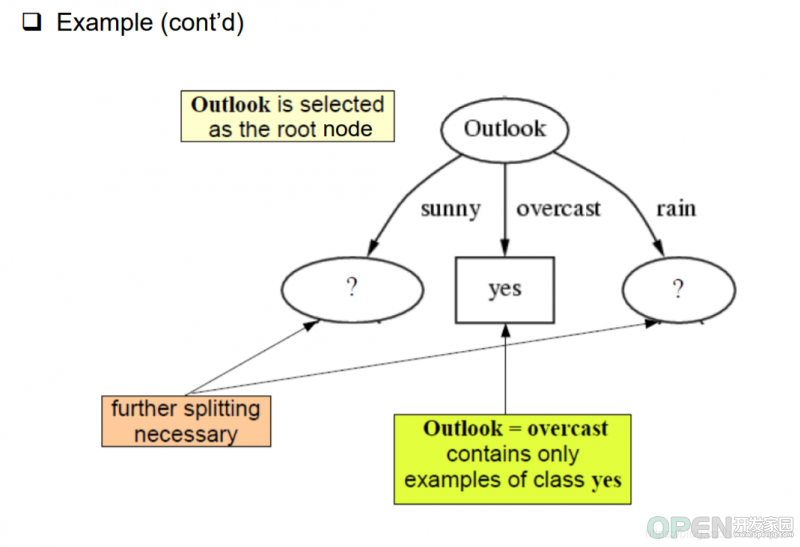
根据上面的计算,我们得到结论outlook优先级高于humidity高于windy。那么在这些影响因素中,outlook成为节点的根,且根据分支,overcast所有预测结果均为yes。
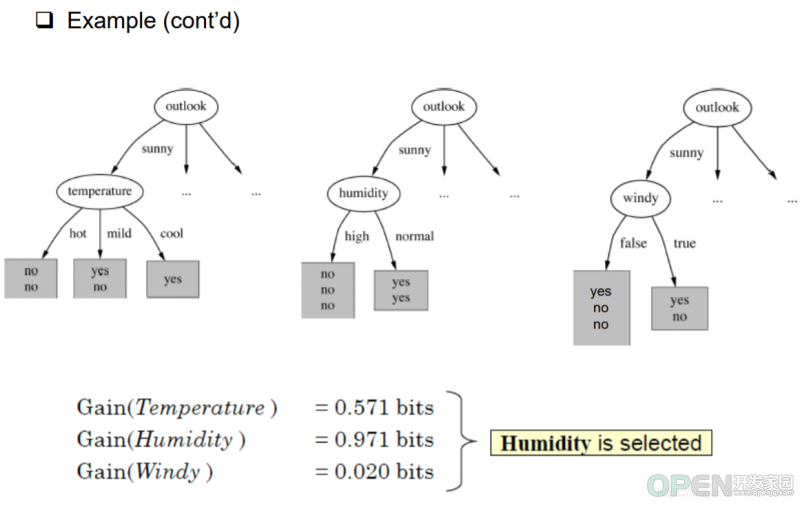
然后我们计算其他因素的信息增益值,就可以找出下位节点。如图所示,是当outlook为sunny时,其他因素的信息增益结果。
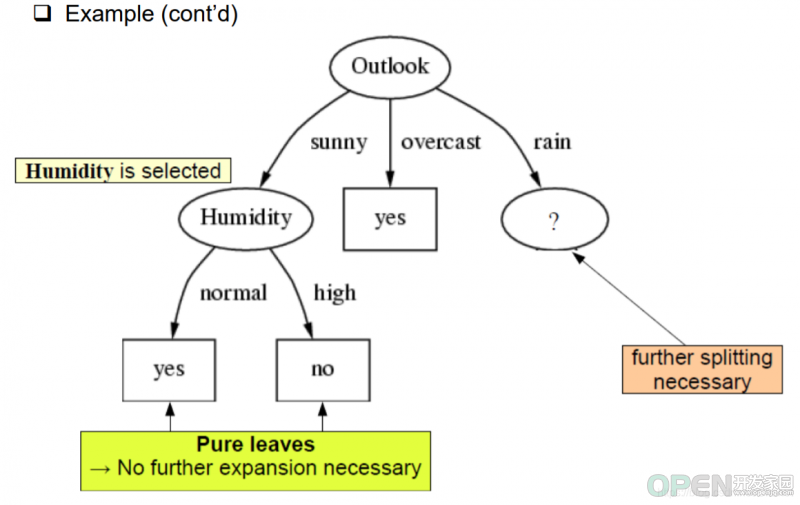
当我们确认下humidity后,再讨论rainy的计算。过程与humidity一样。
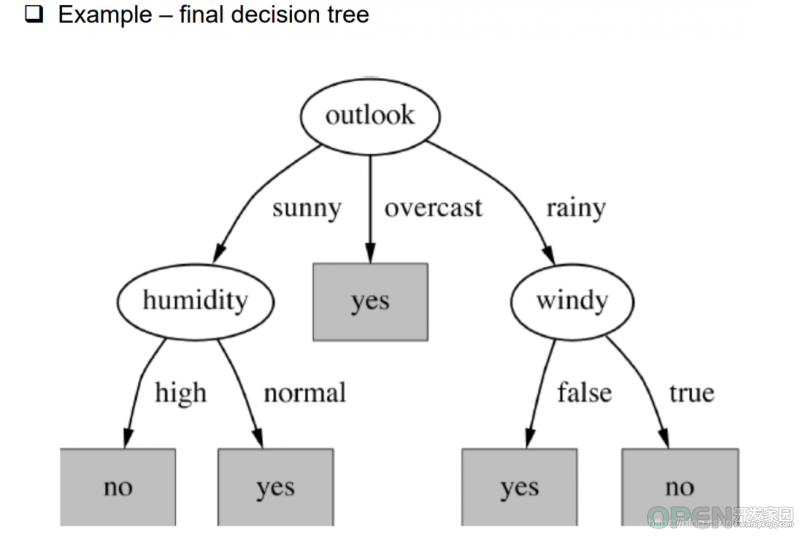
然后我们就可以得到一个新的决策树,而这个决策树比起我们起初设计的决策树简单的多。决策树越简单,效率越高,开销约小。这个例子就直接反映了我们怎么去生成一个高效率的决策树
随机森林简介
随机森林(或随机决策森林):通过在训练时构造多个决策树并输出作为单个树的类的模式的类来集成模型。随机森林的预测只是这些树预测的加权平均值。对于一个分类目标(即分类),这可以是多数投票或基于树产生的概率平均值的最可能值
优势:
- 它能够处理很高维度(feature很多)的数据,并且不用做特征选择
原因:特征子集是随机选择的,子集大小可以控制。
- 在训练完后,它能够给出feature重要大小
- 训练速度快,容易做成并行化方法
原因:训练时树与树之间是相互独立的
- 如果有很大一部分的特征遗失,仍可以维持准确度。
缺陷:
- 随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合
- 对于有不同取值的属性的数据,取值划分较多的属性会对随机森林产生更大的影响,(跟决策树算法类似,以信息增益划分数据集的特征,都有这个问题,可以用信息增益比校正)所以随机森林在这种数据上产出的属性权值是不可信的。
实验

import org.apache.spark.ml.{PipelineModel,Pipeline}
import org.apache.spark.ml.classification.{DecisionTreeClassifier,RandomForestClassifier,RandomForestClassificationModel}
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
import org.apache.spark.ml.feature.{VectorAssembler,VectorIndexer}
import org.apache.spark.ml.linalg.Vector
import org.apache.spark.ml.tuning.{ParamGridBuilder,TrainValidationSplit}
import org.apache.spark.mllib.evaluation.MulticlassMetrics
import org.apache.spark.sql.{DataFrame,SparkSession}
import org.apache.spark.sql.functions._
import scala.util.Random
val dataWithoutHeader = spark.read.option("inferSchema", true).option("header",false).csv("Data/cov/covtype.data" )
dataWithoutHeader.first
dataWithoutHeader.printSchema()
val colNames =Seq(
"Elevation", "Aspect", "Slope" ,
"Horizontal_Distance_To_Hydrology","Yertical_Distance_To_Hydrology" ,
"Horizontal_Distance_To_Roadways",
"HilIshade_9am","Hillshade_Noon","Hillshade_3pm",
"Horizontal_Distance_To_Fire_Points")++
((0 until 4 ).map(i => s"Wilderness_Area_$i"))++
((0 until 40).map(i => s"Soil_Type_$i"))++Seq("Cover_Type")
val data =dataWithoutHeader.toDF(colNames:_* ).withColumn("Cover_Type",$"Cover_Type".cast("double"))
data.printSchema()
val Array(trainData,testData) = data.randomSplit(Array(0.9,0.1))
trainData.cache( )
testData.cache( )
val inputCols = trainData.columns. filter(_!="Cover_Type")
val assembler = new VectorAssembler().setInputCols(inputCols).setOutputCol("featureVector")
val assembledTrainData = assembler.transform(trainData)
assembledTrainData.select("featureVector").show(truncate = false)
val classifier = new DecisionTreeClassifier().
setSeed(Random.nextLong( )).
setLabelCol("Cover_Type").
setFeaturesCol("featureVector").
setPredictionCol("prediction")
val model=classifier.fit(assembledTrainData)
println(model.toDebugString)
model.featureImportances.toArray.zip(inputCols).sorted.reverse.foreach(println)
val predictions = model.transform(assembledTrainData)
predictions.select( "Cover_Type" , "prediction" , "probability").show(truncate = false)
val evaluator = new MulticlassClassificationEvaluator().
setLabelCol("Cover_Type").
setPredictionCol("prediction")
val accuracy = evaluator.setMetricName("accuracy").evaluate(predictions)
val predictionRDD =predictions.
select( "prediction", "Cover_Type").
as[(Double,Double)].rdd
val multiclassMetrics = new MulticlassMetrics(predictionRDD)
println(multiclassMetrics.confusionMatrix)
val classifierHyper = new DecisionTreeClassifier().
setSeed(Random.nextLong()).
setLabelCol( "Cover_Type" ).
setFeaturesCol( "featureVector" ).
setPredictionCol ( "prediction" )
val pipeline = new Pipeline().setStages(Array(assembler,classifierHyper))
val paramGrid = new ParamGridBuilder()
.addGrid(classifier.impurity, Seq("gini", "entropy"))
.addGrid(classifier.maxDepth, Seq(1, 5))
.addGrid(classifier.maxBins, Seq(40, 80))
.addGrid(classifier.minInfoGain, Seq(0.0, 0.05))
.build()
val multiclassEval = new MulticlassClassificationEvaluator().
setLabelCol("Cover_Type").
setPredictionCol("prediction").
setMetricName("accuracy")
val validator = new TrainValidationSplit().
setSeed(Random.nextLong()).
setEstimator(pipeline).
setEvaluator(multiclassEval).
setEstimatorParamMaps(paramGrid).
setTrainRatio(0.9)
val validatorModel=validator.fit(trainData)
val bestModel = validatorModel.bestModel
bestModel.asInstanceOf[PipelineModel].stages.last.extractParamMap
val paramsAndMetrics = validatorModel.validationMetrics.
zip(validatorModel.getEstimatorParamMaps).sortBy(-_._1)
paramsAndMetrics.foreach{case (metric,params)=>
println(metric)
println(params)
println()
}
validatorModel.validationMetrics.max
multiclassEval.evaluate(bestModel.transform(testData))
输出值:res20: Double = 0.6976552151249806
| 
![]() 网络安全
发布于:2021-07-13 17:58
|
阅读数:418
|
评论:0
网络安全
发布于:2021-07-13 17:58
|
阅读数:418
|
评论:0
















 QQ好友和群
QQ好友和群 QQ空间
QQ空间