python 列表的实现探析

太阳不下山

　　知其然也要知其所以然，python中的容器对象真的不多，平常我们会很心安理得的根据需求来使用对应的容器，不定长数据用 list，想去重用 set，想快速进行匹配用 dict，字符处理用 str，可为何能实现这个效果呢？比如我们用 list的时候，知道这玩意可以随意存储各种格式，存整型、浮点、字符串、甚至还可以嵌套 list等其他容器，这底层的原理到底是用数组实现的，还是用链表？比如我们的字典，底层是用数组还是其他？如果是其他如哈希表，那又怎么实现输入数据的顺序排列？这次不妨一层层剖析，推演一番。贪多嚼不烂，本次就先对 list进行分析

简述

　　这个名字很容易和其它语言（C++、Java等）标准库中的链表混淆，不过事实上在 CPython的列表根本不是列表（这话有点绕，可能换成英文理解起来容易些：python中的list不是我们所学习的list），在CPython中，列表被实现为长度可变的数组。
　　从细节上看，Python中的列表是由对其它对象的引用组成的连续数组，指向这个数组的指针及其长度被保存在一个列表头结构中。这意味着，每次添加或删除一个元素时，由引用组成的数组需要该标大小（重新分配）。在实现过程中，Python在创建这些数组时采用了指数分配的方式，其结果导致每次操作不都需要改变数组的大小，但是也因为这个原因添加或取出元素的平均复杂度较低。
　　这个方式带来的后果是在普通链表上“代价很小”的其它一些操作在Python中计算复杂度相对过高。

利用 list.insert(i,item) 方法在任意位置插入一个元素——复杂度O(N)
利用 list.pop(i) 或 list.remove(value) 删除一个元素——复杂度O(N)

源码解析

　　让我们先看下list实现的源码，源汁源味，细细品评。我们先发现list多重继承自 MutableSequence 和 Generic。之后我们可以读到，list的相关内嵌函数的实现，如append、pop、extend、insert等其实都是通过继承来实现的，那么我们就不得不去找一下 MutableSequence 和 Generic这两个类的实现底层，也只有解答了这两个类之后，我们才能回答为何list可以实现动态添加数据，而且删除和插入的复杂度还不是那么优秀。

class list(MutableSequence[_T], Generic[_T]):
  @overload
  def __init__(self) -> None: ...
  @overload
  def __init__(self, iterable: Iterable[_T]) -> None: ...
  if sys.version_info >= (3,):
    def clear(self) -> None: ...
    def copy(self) -> List[_T]: ...
  def append(self, object: _T) -> None: ...
  def extend(self, iterable: Iterable[_T]) -> None: ...
  def pop(self, index: int = ...) -> _T: ...
  def index(self, object: _T, start: int = ..., stop: int = ...) -> int: ...
  def count(self, object: _T) -> int: ...
  def insert(self, index: int, object: _T) -> None: ...
  def remove(self, object: _T) -> None: ...
  def reverse(self) -> None: ...
  if sys.version_info >= (3,):
    def sort(self, *, key: Optional[Callable[[_T], Any]] = ..., reverse: bool = ...) -> None: ...
  else:
    def sort(self, cmp: Callable[[_T, _T], Any] = ..., key: Callable[[_T], Any] = ..., reverse: bool = ...) -> None: ...
  def __len__(self) -> int: ...
  def __iter__(self) -> Iterator[_T]: ...
  def __str__(self) -> str: ...
  __hash__: None  # type: ignore
  @overload
  def __getitem__(self, i: int) -> _T: ...
  @overload
  def __getitem__(self, s: slice) -> List[_T]: ...
  @overload
  def __setitem__(self, i: int, o: _T) -> None: ...
  @overload
  def __setitem__(self, s: slice, o: Iterable[_T]) -> None: ...
  def __delitem__(self, i: Union[int, slice]) -> None: ...
  if sys.version_info < (3,):
    def __getslice__(self, start: int, stop: int) -> List[_T]: ...
    def __setslice__(self, start: int, stop: int, o: Sequence[_T]) -> None: ...
    def __delslice__(self, start: int, stop: int) -> None: ...
  def __add__(self, x: List[_T]) -> List[_T]: ...
  def __iadd__(self: _S, x: Iterable[_T]) -> _S: ...
  def __mul__(self, n: int) -> List[_T]: ...
  def __rmul__(self, n: int) -> List[_T]: ...
  if sys.version_info >= (3,):
    def __imul__(self: _S, n: int) -> _S: ...
  def __contains__(self, o: object) -> bool: ...
  def __reversed__(self) -> Iterator[_T]: ...
  def __gt__(self, x: List[_T]) -> bool: ...
  def __ge__(self, x: List[_T]) -> bool: ...
  def __lt__(self, x: List[_T]) -> bool: ...
  def __le__(self, x: List[_T]) -> bool: ...

MutableSequence

　　这个类其实是来自于 collections.abc.MutableSequence，其实也就是所谓的抽象基础类里面的可变序列的方法。
　　Python的序列有两种，可变序列和不可变序列并为其提供了两个基类 Sequence和 MutableSequence，这两个基类存在于内置模块 collections.abc中，与其他常见的类如 int、 list等不同，这两个基类都是抽象基类。这里涉及到一个新的概念抽象基类，什么是抽象基类呢？
　　对于抽象基类，目前可以不用关注太多，只需知道抽象基类是指不能实例化产生实例对象的类，后面有机会我们再专门来讨论抽象基类。
Sequence和 MutableSequence是两个抽象基类，因此这两个类都是不能实例化产生实例对象，那要 Sequence和 MutableSequence两个抽象基类还有什么作用呢？　　其实抽象基类的作用并不是实例化产生实例对象的，它的作用更多的像是定义一种规则，或者官方的说法叫做协议，这样以后我们希望创建这种类型的对象时，要求遵循这种规则或者协议。现在我们需要了解序列类型都有哪些协议，这需要学习abc模块中的 Sequence和 MutableSequence两个类。
　　Sequence和MutableSequence两个类的继承关系如下：

　　是否是通过链表结构实现的呢? 毕竟链表支持动态的调整，借助于指针可以引用不同类型的数据，比如下面的图示中的链表结构。但是这样的话使用下标索引数据的时候，需要依赖于遍历的方式查找，O(n)的时间复杂度访问效率实在是太低。
　　不过对于链表的使用，系统开销也较大，毕竟每个数据项除了维护本地数据指针外，还要维护一个 next指针，因此还要额外分配8字节数据，同时链表分散性使其无法像数组一样利用CPU的缓存来高效的执行数据读写。

　　实现的细节可以从其Python的源码中找到，定义如下：

typedef struct {
  PyObject_VAR_HEAD
  PyObject **ob_item;
  Py_ssize_t allocated;
} PyListObject;

　　内部list的实现的是一个C结构体，该结构体中的 ob_item是一个指针数组，存储了所有对象的指针数据， allocated是已分配内存的数量, PyObject_VAR_HEAD是一个宏扩展包含了更多扩展属性用于管理数组，比如引用计数以及数组大小等内容。

动态数组

　　既然是一个动态数组，则必然会面临一个问题，即如何进行容量的管理，大部分的程序语言对于此类结构使用动态调整策略，也就是当存储容量达到一定阈值的时候，扩展容量，当存储容量低于一定的阈值的时候，缩减容量。道理很简单，不过实施起来可没那么容易，什么时候扩容，扩多少，什么时候执行回收，每次又要回收多少空闲容量，这些都是在实现过程中需要明确的问题。
　　对于Python中list的动态调整规则程序中定义如下：当追加数据容量已满的时候，通过下面的方式计算再次分配的空间大小，创建新的数组，并将所有数据复制到新的数组中。这是一种相对数据增速较慢的策略，回收的时候则当容量空闲一半的时候执行策略，获取新的缩减后容量大小。其实这个方式就很像TCP的滑动窗口的机制

new_allocated = (newsize >> 3) + (newsize < 9 ? 3 : 6);
 
new_allocated += newsize
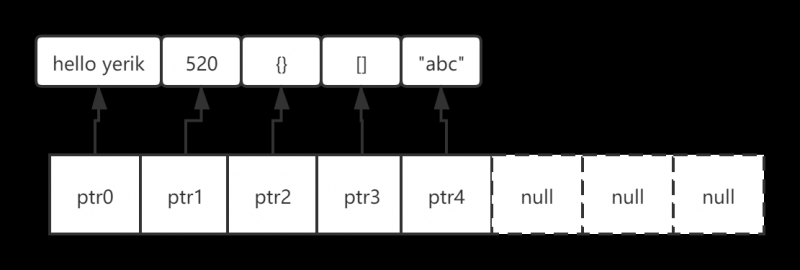
//  0, 4, 8, 16, 25, 35, 46, 58, 72, 88, …

　　假如我们使用一种最简单的策略：超出容量加倍，低于一半容量减倍。这种策略会有什么问题呢？设想一下当我们在容量已满的时候进行一次插入，随即删除该元素，交替执行多次，那数组数据岂不是会不断的被整体复制和回收，已经无性能可言了。

append

　　接下来，我们来看下list数据结构的几个常见操作。首先是在list上执行append的操作，该函数将元素添加到list的尾部。注意这里是指针数据被追加到尾部，而不是实际元素。

test = list()
test.append("hello yerik")

　　向列表添加字符串：test.append("hello yerik") 时发生了什么？实际上是调用了底层的 C 函数 app1()。

arguments: list object, new element
returns: 0 if OK, -1 if not
app1:
  n = size of list
  call list_resize() to resize the list to size n+1 = 0 + 1 = 1
  list[n] = list[0] = new element
  return 0

　　对于一个空的list，此时数组的大小为0，为了能够插入元素，我们需要对数组进行扩容，按照上面的计算公式进行调整大小。比如这时候只有一个元素，那么newsize = 1, 计算的new\_allocated = 3 + 1 = 4 ，成功插入元素后，直到插入第五元素之前我们都不需要重新分配新的空间，从而避免频繁调用 list_resize() 函数，提升程序性能。

insert

　　在列表偏移量 2 的位置插入新元素，整数 5：test.insert(1,2.33333333)，内部调用ins1() 函数。

arguments: list object, where, new element
returns: 0 if OK, -1 if not
ins1:
  resize list to size n+1 = 5 -> 4 more slots will be allocated
  starting at the last element up to the offset where, right shift each element 
  set new element at offset where
  return 0

　　python实现的insert函数接收两个参数，第一个是指定插入的位置，第二个为元素对象。中间插入会导致该位置后面的元素进行移位操作，由于是存储的指针因此实际的元素不需要进行位移，只需要位移其指针即可。

>>> test.insert(2,2.33333333)
>>> test
['hello yerik', 520, 2.33333333, {}, [], 'abc']

　　pop的操作也是需要进行检查缩小，因此也是导致复杂度为O(n)

Remove

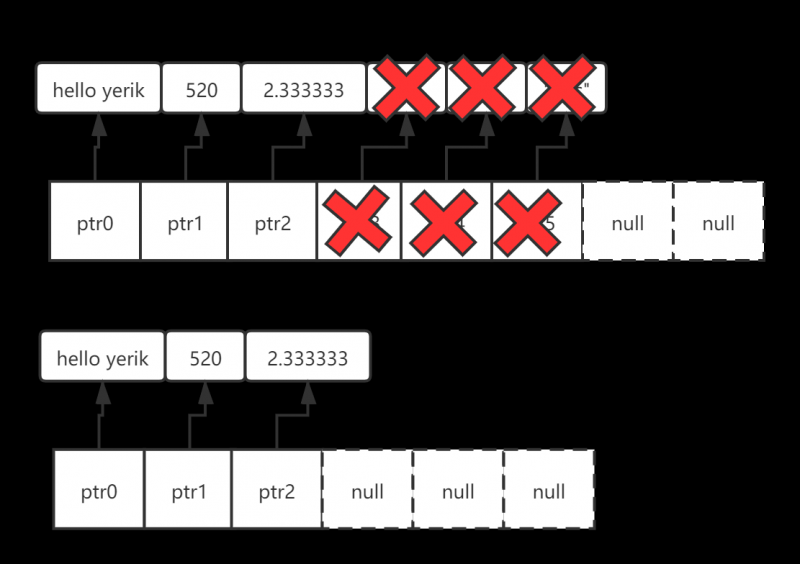
　　remove函数会指定删除的元素，而该元素可以在列表中的任意位置。因此每次执行remove都必须先依次遍历数据项，进行匹配，直到找到对应的元素位置。执行删除可能会导致部分元素的迁移。Remove操作的整体时间复杂度为O(n)。

[python] python 列表的实现探析

相关帖子

学会这些linux的“自动化”轻松搞定任务

终究还是错付了！这2种Python写法已经被淘汰了，你是不是还在用？

Linux下玩转nginx系列（八）---如何使用upsync模块实现动态负载均衡

Mysql8导入数据到Mysql5.7的实现步骤

javascript怎么实现窗口置顶

JavaScript怎样实现点击出现图片效果

Android控件Spinner实现下拉列表及监听功能

基于python的动态时钟，带十二时辰和经络养身

使用原生querySelectorAll和forEach来实现点击切换

免插件、DZ内置JS轻松实现外链访问二次确认对话提示框

太阳不下山 LV4