[通信技术]
《信号与系统》解读 第3章 强大的傅里叶时域频域分析工具-3:时域信号的傅里叶变换与常见信号的频谱
 网络安全
发布于:2021-07-27 14:01
|
阅读数:838
|
评论:0
网络安全
发布于:2021-07-27 14:01
|
阅读数:838
|
评论:0
|
|
目录
目录
1 时域周期性信号的频域傅里叶级数概述
1.1 周线性、连续信号的傅里叶级数
1.2 周期、离散信号的傅里叶级数
2 时域、周期性、连续信号的频域傅里叶级数的频谱图表达
2.1 周期性、连续信号的频谱图
2.2 周期性、离散信号的频谱图
3 时域、周期性、连续信号的频域傅里叶级数的三角函数表达式
3.1 周期性、连续信号
3.2 周期性、离散信号
4 时域、周期性、连续信号的频域傅里叶级数的复指数表达式
4.1 周期性、连续信号
4.2 周期性、离散信号
5 傅里叶级数参数的量化
5.1 周期性、连续信号
5.2 周期性、离散信号
6 常见时域、周期性、连续信号的频域傅里叶级数案例
1 时域周期性信号的频域傅里叶级数概述
1.1 周线性、连续信号的傅里叶级数
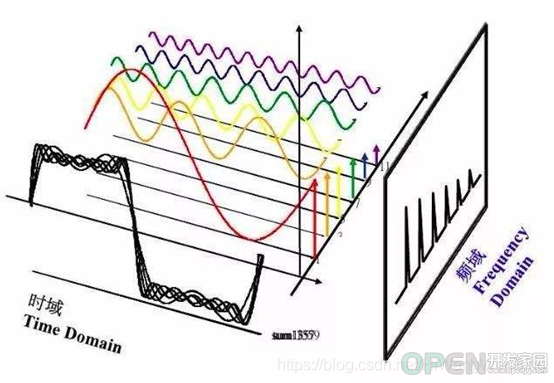
傅里叶分析认为:
时间上连续的、任意周期的时域信号可以分解为无限多个、离散的、非周期的、正交的复指数频域信号之和,称之为傅里叶级数。
为什么会有这个结论呢?
从定性的角度来看,周期信号是有规律的复杂信号,而频率具有倍数关系的正弦信号序列cos(n*ωt)+ i*sin(n*ωt)是具有规律的基本信号。
用无数个不同幅度的、有规律的、基本信号叠加,获得有规律复杂的周期信号,是可行的。
1.2 周期、离散信号的傅里叶级数
傅里叶分析认为:
时间上离散的、任意周期的时域信号可以分解为无限多个、离散的、周期的、正交的复指数频域信号之和,称之为离散傅里叶级数。
也就是说,周期性的离散信号,相对于周期性的连续信号而言,其频谱比连续信号的频谱更有规律性,也变成了周期信号。
所谓频谱的周期性,是指不同频率分量的幅度呈现周期性特点,而不像周期连续信号,其频谱是没有周期的。
1.3 非周期连续信号
傅里叶认为,时域非周期连续信号的频谱可以由周期连续信号的频谱推导而来。
当时域信号的周期无穷大时,周期信号就变成了非周期信号。周期无限大,就意味着时域信号的频率小,也就意味着,基波频率就无限小,同时意味着两个相邻的谐波信号之间的间距就无限小,间距无穷小,就意味着谐波的频率变成了连续。
也可以这样理解,周期信号是规律性信号,因此可以通过无限个、离散的、谐波信号组合而成,当变成无规律的非周期信号时,就需要更多的谐波信号组合而成,多到谐波频率在整个数轴空间是连续的!
2 时域、周期性、连续信号的频域傅里叶级数的频谱图表达
2.1 周期性、连续信号的频谱图
周期连续信号有2个重要的参数:
T > τ
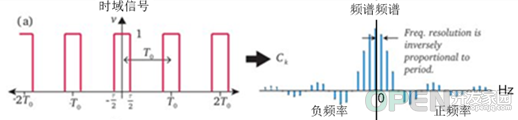
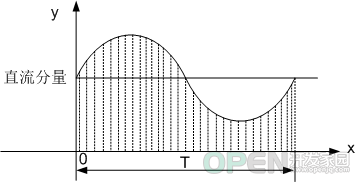
(1)时域信号
右边是时域信号,这里周期性的脉冲信号。
(2)频域频谱
右边是对应的傅里叶级数的频谱图,代表时域信号中包含的不同频率的复指数信号(正弦信号)的频率n*ωt以及其对应的幅度。
- 其中n=0的幅度表示直流分量
- 其中n=1的幅度表示基波频率分量
- 其中n>1的幅度表示其他的谐波分量
- 幅度是可以为负数的:如 -1 * cos(n*ωt) - i*sin(n*ωt)
- 频率是可以为负数的:频率为正数,表示逆时针旋转,频率为负数,表示顺时针旋转。
关于复指数信号的负幅度和负频率,请参考:
《星星之火-35:为什么傅里叶分析需要引入负频率以及负频率的物理意义是什么?》
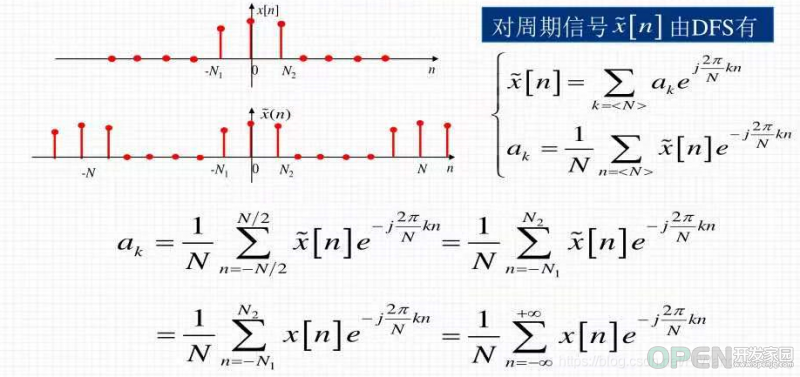
2.2 周期性、离散信号的频谱图
周期离散信号有2个重要的参数:
- 信号周期内,全部采样的个数N
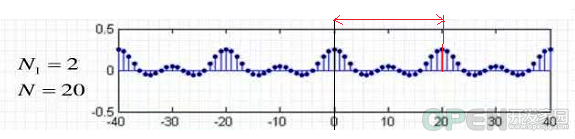
- 信号周期内,有效信号的采样的个数N1
N>N1.
如下是N=20, N1=2时的离散方波信号的频谱图:
从上图可以看出,:
这与周期连续信号一样,表明时域信号内含的谐波频率是离散的。
这与周期连续信号不同,周期连续信号,各个频率分量的幅值是递减的,无周期性;
而周期离散信号,各个频率分量的幅度是呈现周期性变化。
周期的大小,取决于相邻两个采样点的时间间隔,
采样的时间越小,离散的点越密集,
采样的频率越大,当采样点无限密集,就接近周期连续信号,频谱的周期也就接近无穷大,即呈现周期连续信号的频谱的非周期性特点了。
这与周期连续信号不同,周期连续信号,也就是在一个周期T内,连续信号的采样点相当于是无限的,因此其频谱,虽然是离散的,谐波分量的个数是无限的;
而周期离散信号, 在一个周期内的采样点的个数是有限的,因此其频谱也是有限的,有限性体现在其周期性上,频谱的谐波分量的个数,就是频谱周期内的谐波数。
频谱的有限性是周期性离散信号的一个很重要的优点,通过有限的谐波频率,就可再现周期性离散信号,节省了网络带宽。
时域的离散性是周期性离散信号的另一个很重要的优点,而累积和替代连续信号的积分,非常便于计算机处理。
周期性离散信号是计算机数字通信中最重要的一种时域信号形式。
在计算机数字信号处理中,对于连续信号,也先通过采样的手段,把连续信号先转换成离散信号。采样后,不仅仅利于计算机处理,还节省了恢复信号是所需的频谱资源。
2.3 非周期、连续信号
从频谱上看,时域上非周期、连续信号信号,其基波信号的频率是无限接近于0,相邻谐波信号的频率间隔接近于0,是频谱是连续的。
2.4 非周期、离散信号
时域的非周期性导致频域频谱的连续性,需要无线连续的谐波分量来组合没有规律的时域非周期信号。
时域的离散性导致频域频谱的周期性,规律性,这是时域离散性带来的好处。
3 时域、周期性、连续信号的频域傅里叶级数的三角函数表达式
3.1 周期性、连续信号
假设时域周期连续信号f(t)的周期为T
此级数公式表明:时域信号f(t)可以由无数个频域的正弦信号组成。
3.2 周期性、离散信号
3.3 非周期、连续信号
3.4 非周期、离散信号
4 时域、周期性、连续信号的频域傅里叶级数的复指数表达式
4.1 周期性、连续信号
此级数公式表明:时域信号f(t)可以由无数个频域的复指数信号组成。
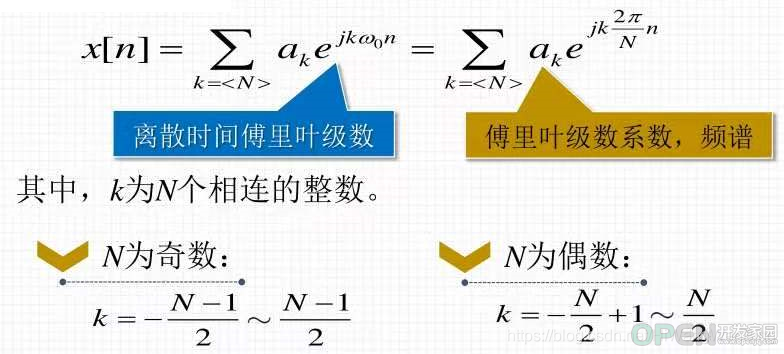
4.2 周期性、离散信号
(1)傅里叶级数复指数信号集
(2)傅里叶级数复指数表达
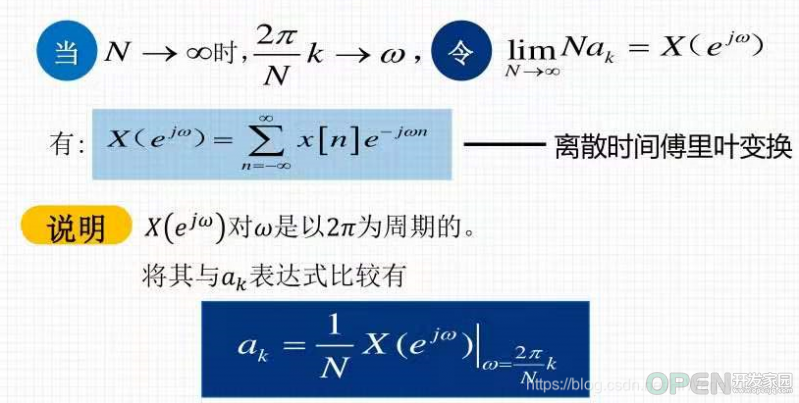
4.3 非周期、连续信号
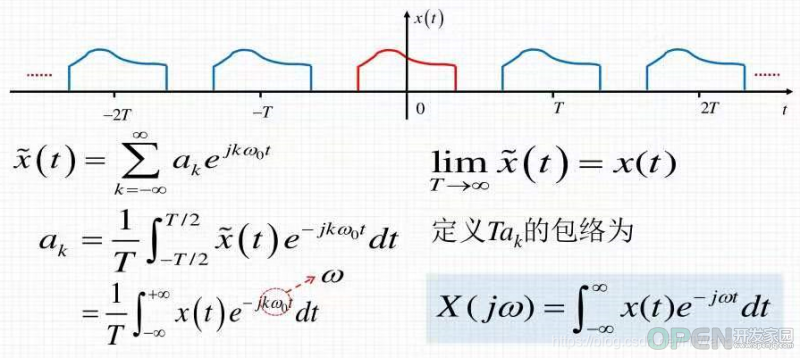
上述数学表达式表示:
时域上没有规律的非周期连续信号,由无限多个谐波信号
 构成,每个信号的频率ω是一个挨着一个的、连续的,频率间隔无限小或者说没有间隔,因此n =》dω,用, 因此每个谐波信号的幅度也不在是离散的,而是连续的,用X(jw)表示,因为没有谐波频率之间没有时间间隔,因此了积分
构成,每个信号的频率ω是一个挨着一个的、连续的,频率间隔无限小或者说没有间隔,因此n =》dω,用, 因此每个谐波信号的幅度也不在是离散的,而是连续的,用X(jw)表示,因为没有谐波频率之间没有时间间隔,因此了积分
 替代了累计和
替代了累计和
 。
。
4.4 非周期、离散信号
非周期、离散信号可以由周期、离散信号演变而来,扩展周期离散信号的周期到无穷大。
5 傅里叶级数参数的量化
5.1 周期性、连续信号
为了简化讨论,这里以正频率为例,负频率是与正频率对称的,有一个正频率ω,就有一个对应的负频率-ω。
(1)频率的量化:
- 直流分量的频率 :n=0, n*ω = 0;
- 正弦基波的频率: n=1, ω = 1* ω = 2πf = 2π/T;
- 正弦谐波的频率: n>1, ωn = n * ω = n* 2π/T
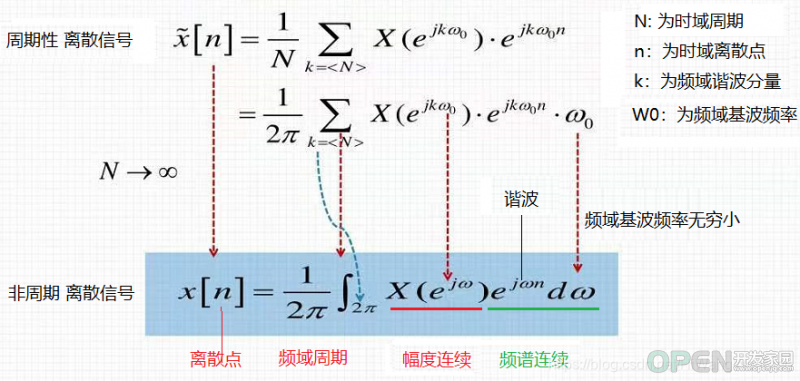
(2)幅度的量化
5.2 周期性、离散信号
5.3 非周期性、连续信号
由于非周期连续信号的频谱是连续的,其幅度不再用Ak表示,是而是X(jω)表示,X是jω的复变函数。
5.4 非周期性、离散信号
6 常见时域、周期性、连续信号的频域傅里叶级数案例
6.1 周期性连续信号
(1)普通正弦函数的频谱图
单一频率的正弦或余弦信号,又称为单音信号。
可以用三角函数表示,此时的频谱是单一的正频率。
正弦信号或余弦信号本身也可以用复指数表示:包括一对绝对值相等、符号相反的频率。
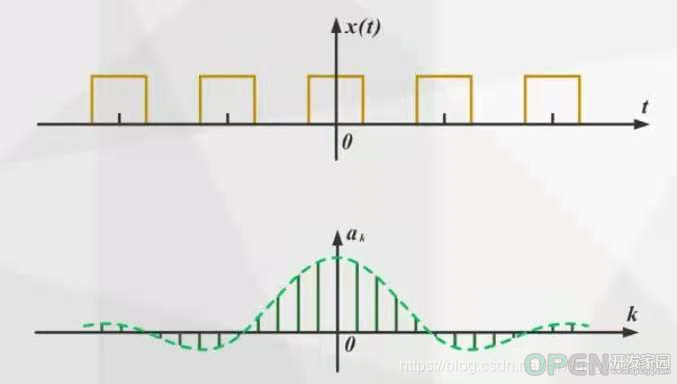
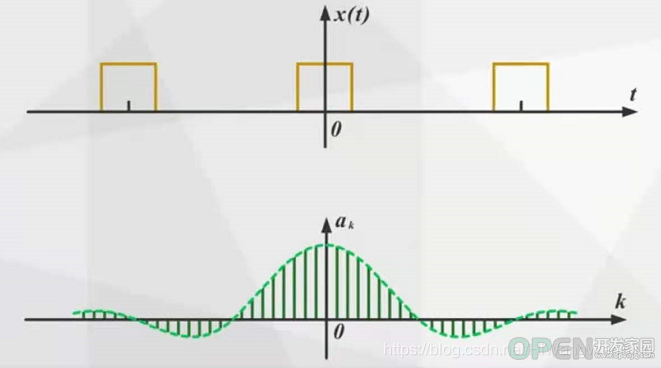
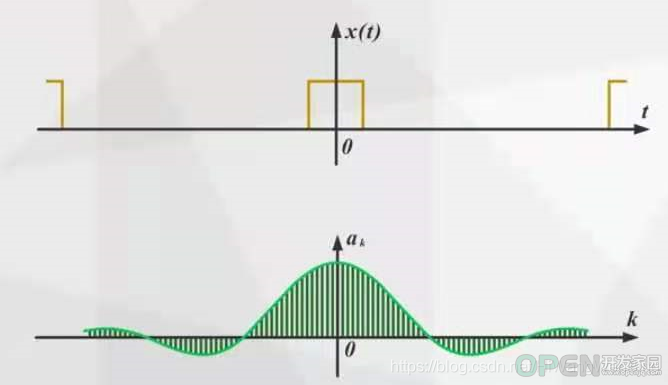
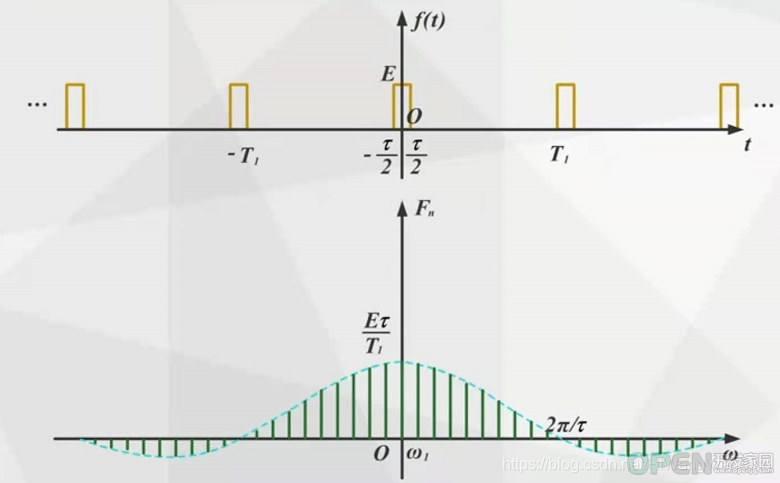
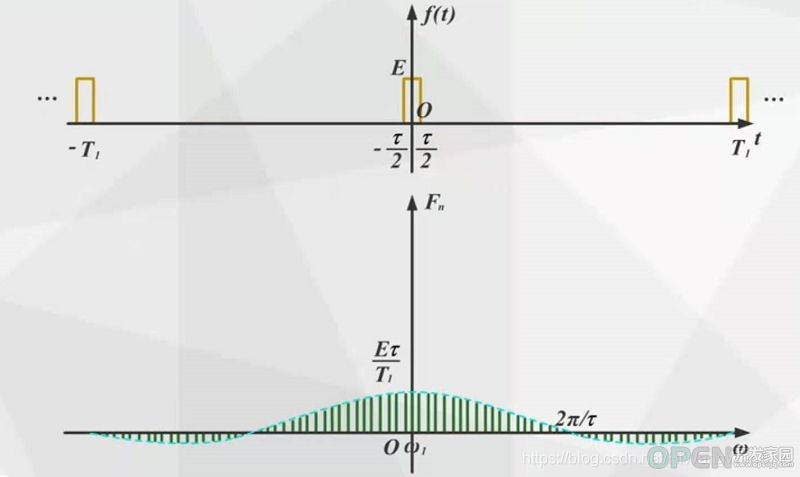
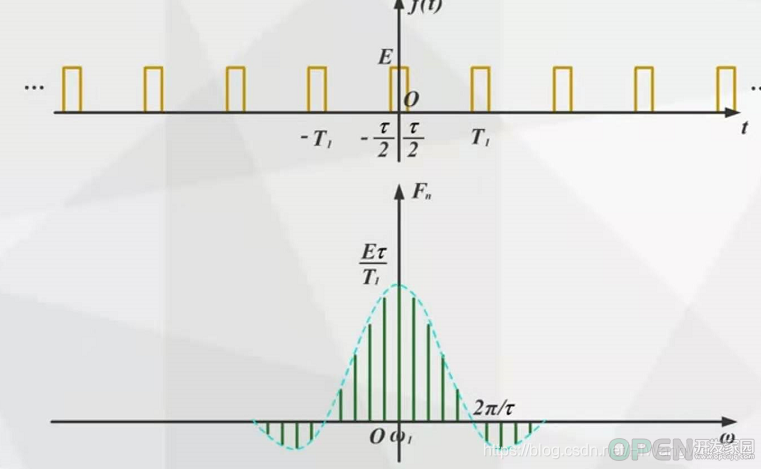
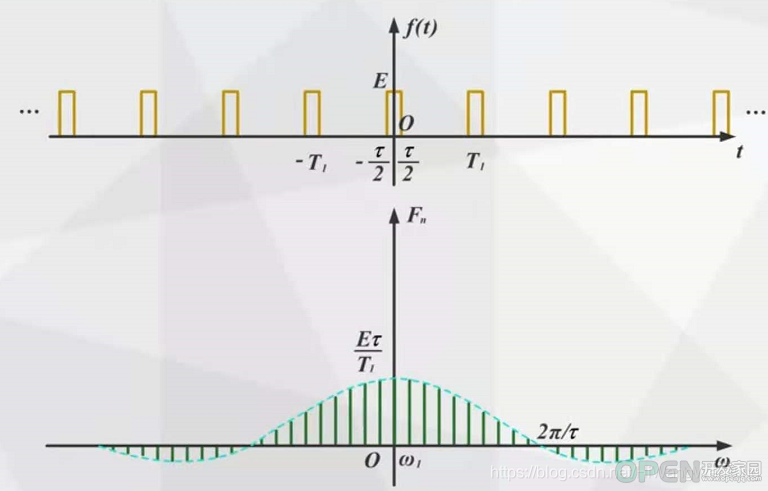
(2)周期矩形脉冲信号
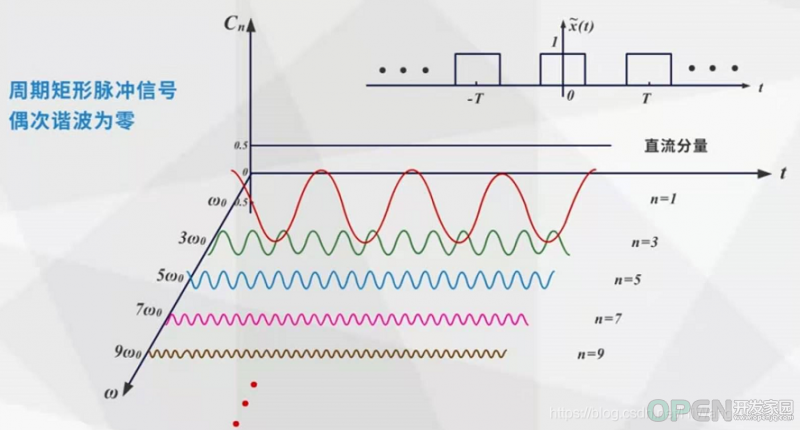
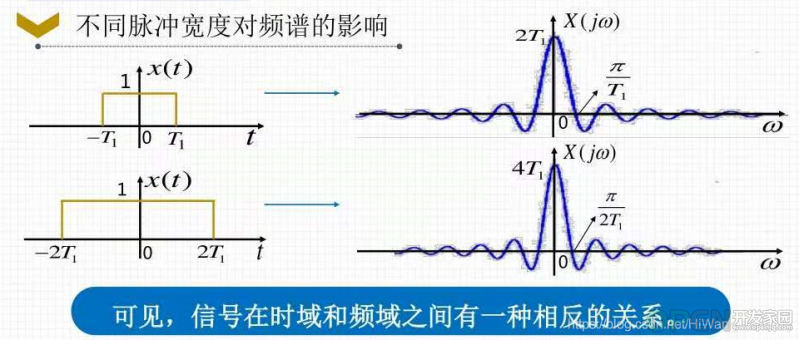
脉冲宽度不变,时域信号的周期T变化,影响的频域信号的基波频率和各个谐波信号的频率。T越大,基波频率越小,谐波频率越密集。
周期不变,时域信号脉冲宽度t, 影响的是时域信号在周期内T内的积分值。 t越大,一个周内内的能量越大,各个谐波分量的幅度就越大。
(3)周期三角脉冲信号
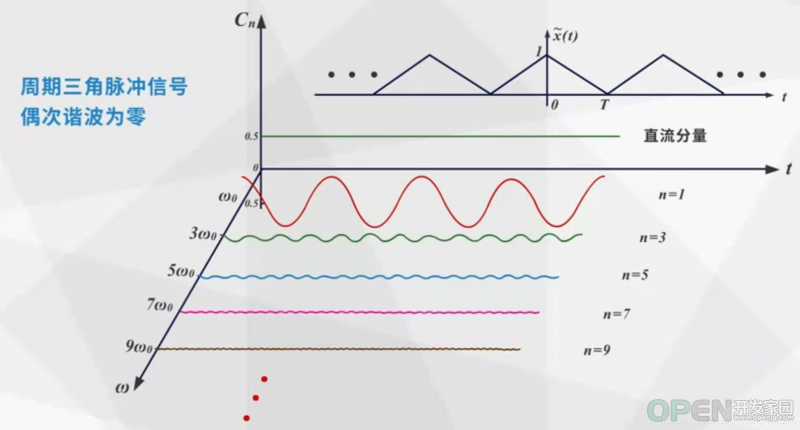
6.3 非周性连续信号
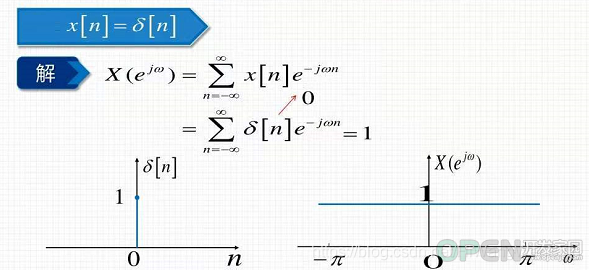
(1)冲击脉冲信号
时域上看,持续时间无穷小。
频域上看,包含所有频率值的谐波,频率值是连续。每个谐波频率的幅度为1.
也可以这样理解:脉冲信号,是瞬间发生、瞬间消失的脉冲信号,因此其频率变化无穷大,因此包含频率值从0到无穷大的所有的谐波分量。
(2)直流分量
时域上看:可以看成是周期无穷小的信号信号,导致其幅度值一直不变化。
频域上看:因为信号的幅度一直不变化,说明此时域信号不包含任何频率ω会发生变化的交流分量,说明只包含频率ω=0的分量,即直流分量。
这就是为什么,频谱图上只看到ω=0处的幅度。
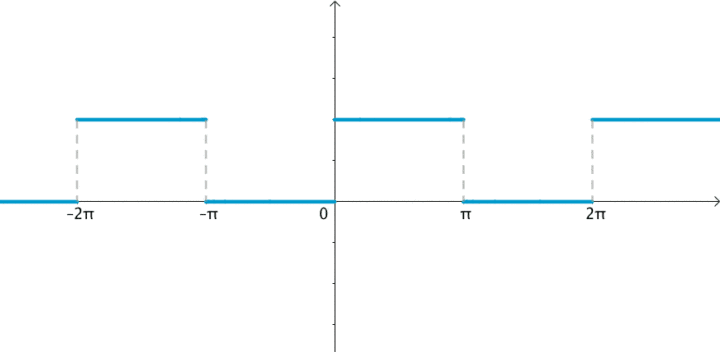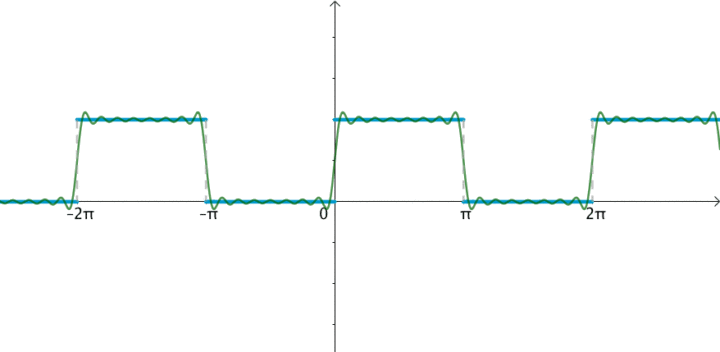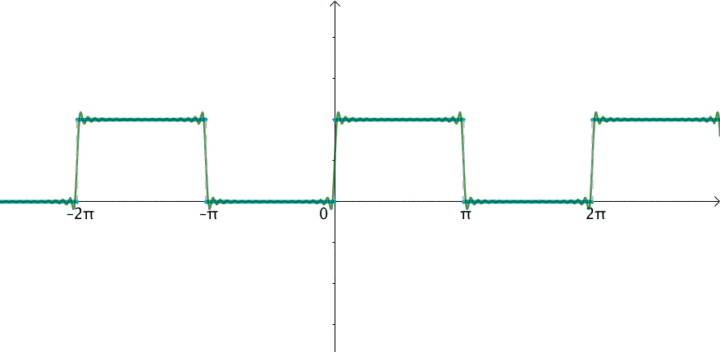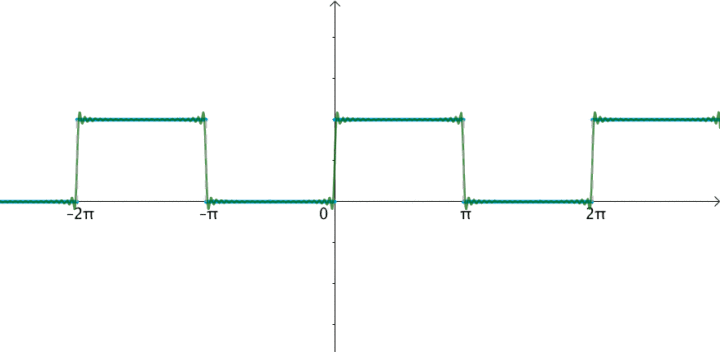
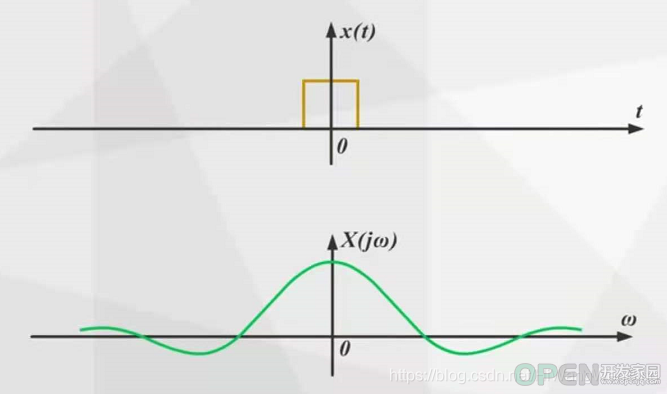
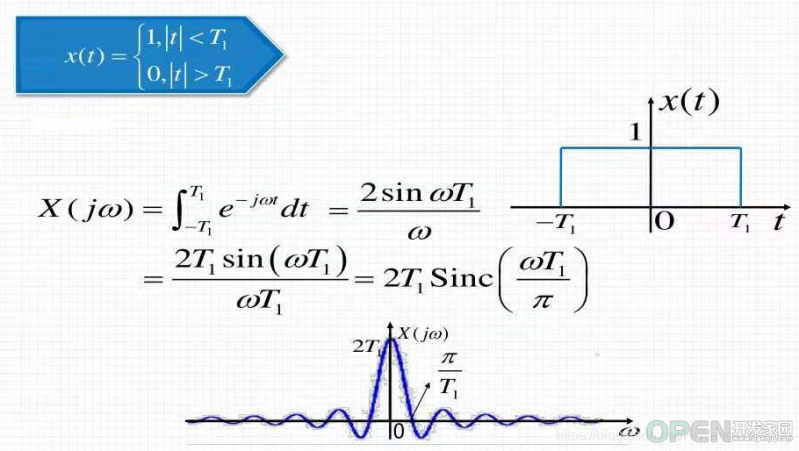
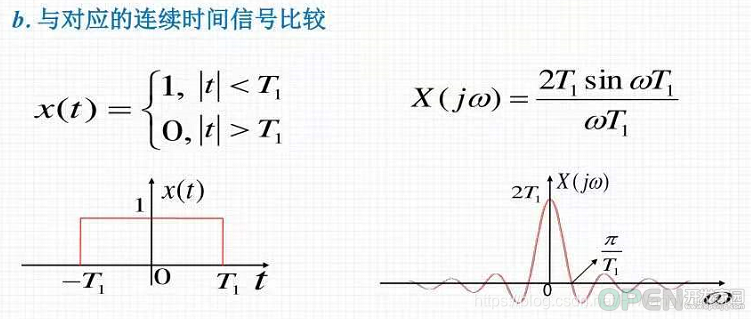
(3)单位矩形脉冲
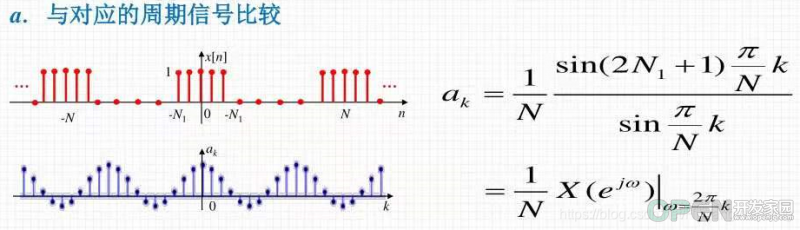
很显然,单个的矩形脉冲与周期性的矩形矩形脉冲:
相同点:图形的包络是相似的。都是sinc函数,即辛格函数。注意:不是sin函数。
区别是:单个的矩形脉冲的频谱是连续的,周期性的矩形矩形脉冲的频谱是离散的。
6.4 非周性离散信号
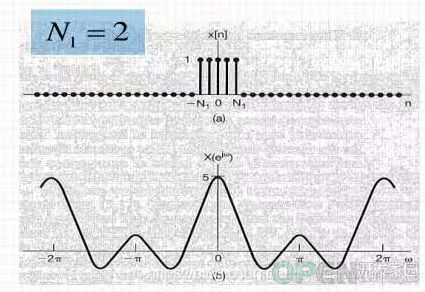
(1)单位脉冲信号
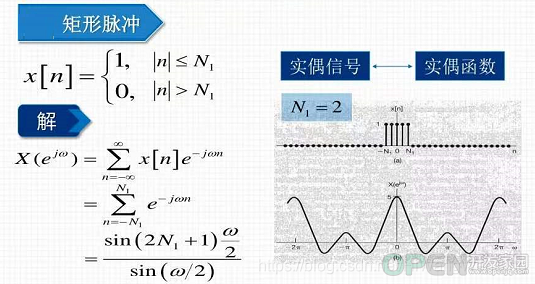
(2)矩形脉冲信号
其他参考:
(1)sinc函数
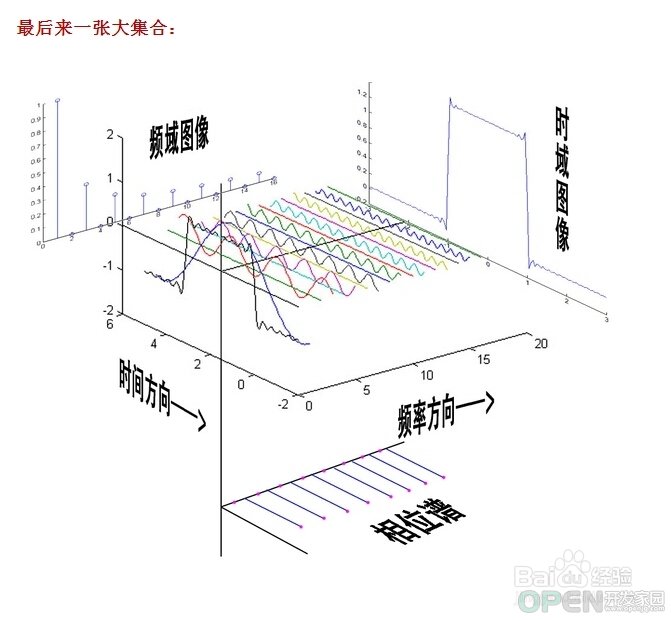
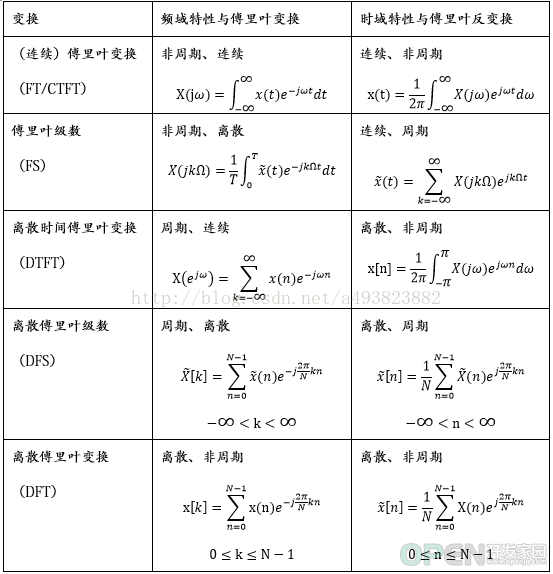
(2) 不同变换汇总
|
免责声明:
1. 本站所有资源来自网络搜集或用户上传,仅作为参考不担保其准确性!
2. 本站内容仅供学习和交流使用,版权归原作者所有!© 查看更多
3. 如有内容侵害到您,请联系我们尽快删除,邮箱:kf@codeae.com
|
|
|
|
|
|
|
|
|

![]() 网络安全
发布于:2021-07-27 14:01
|
阅读数:838
|
评论:0
网络安全
发布于:2021-07-27 14:01
|
阅读数:838
|
评论:0



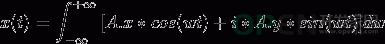

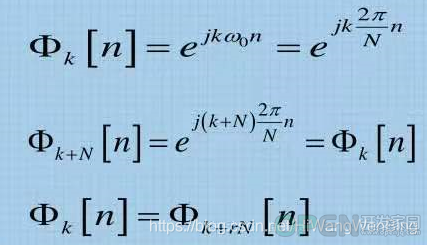

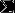


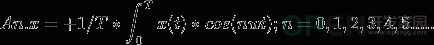
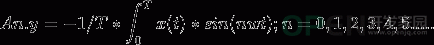





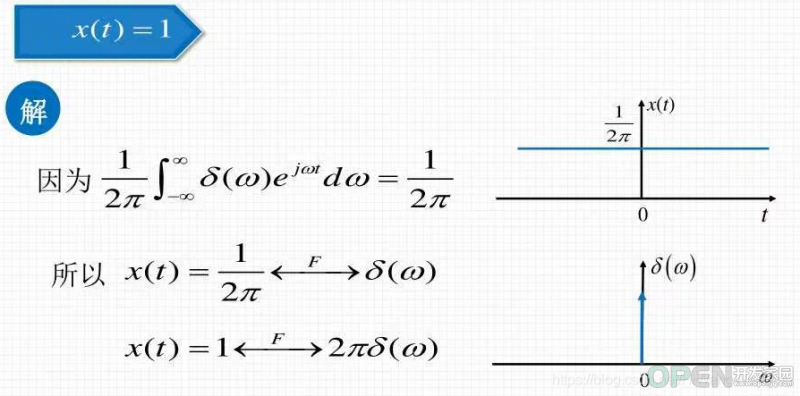
 QQ好友和群
QQ好友和群 QQ空间
QQ空间