阶乘的增长和解决方案

Green

讨论在C#环境下阶乘的增长速度和如何实现更大整数的阶乘
阶乘的增长许多程序设计的书上都有介绍阶乘，我相信包括我在内的人都是看过即可，没有深入的想过其他的问题。比如在整数的范围内（以C#）为例，阶乘究竟可以计算到多大。
下面以一段代码测试下：

int total = 1;
      for (int i =

1

; i <= 20; i++)
      {
        total *= i;
        Console.WriteLine("{0}\t{1}",i,total);
      }

结果如下：

可以发现，在17就明显出问题了，再仔细观察，在14的时候也有问题，14的阶乘居然没有13的阶乘大。我们再用C#的checked关键字验证一下，发现运算到13的时候就出现溢出了。
大家都知道“指数爆炸”，在int类型的取值范围内，我们取2的指数最多可以取到30，但是阶乘最多只能取到12。可见，阶乘的增长比指数快多了。在网上找了一张各个函数增长率的图，如下：

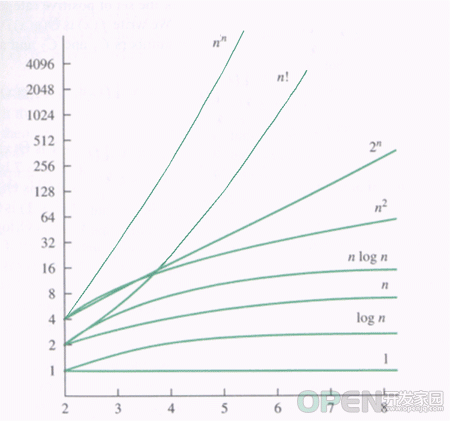
大整数阶乘的解决乘法本质上是加法运算，回顾我们小学的知识。被乘数乘上乘数就是乘数的各位依次与被乘数相乘再求和。例如：11*11=10*11+1*11。这样我们就可以将大数的乘法化为小数的乘法与加法。只要乘数不大于int的最大值的九分之一即可（超过九分之一则会发生溢出）。这样就可以利用乘法计算阶乘了。
代码下面是我所写的乘法类，代码较简单，关键部分有注释，就不详细解释了。

/// <summary>
  /// 乘法类,可用于计数小于Int32.MaxValue十分之一的乘法
  /// </summary>
  public class Multiplication
  {
    #region Fields
    /// <summary>
    /// 保存乘法结果的数组
    /// </summary>
    private int[] _result = new int[4];
    /// <summary>
    /// 被乘数的最高位
    /// </summary>
    private int _topDigit = 3;
    /// <summary>
    /// 最大的被乘数
    /// </summary>
    public const int MaxMultiplier = Int32.MaxValue / 9;
    #endregion Fields
    #region Properties
    /// <summary>
    /// 获取结果枚举器,按从高位到低位
    /// </summary>
    public IEnumerable<int> Result
    {
      get { return _result.Skip(_topDigit); }
    }
    #endregion Properties
    #region Public Methods
    #region  Constructs
    /// <summary>
    /// 使用被乘数为1构造乘法类
    /// </summary>
    public Multiplication()
    {
      //初始化为1 
      _result[_result.Length - 1] = 1;
    }
    /// <summary>
    /// 使用指定的被乘数构造乘法类
    /// </summary>
    /// <param name="multiplicand">被乘数</param>
    public Multiplication(int multiplicand)
      : this()
    {
      Multiply(multiplicand);
    }
    #endregion Constructs
    #region Operators
    /// <summary>
    /// 重载乘法运算符
    /// </summary>
    /// <param name="multiplication">乘法类</param>
    /// <param name="multiplier">乘数,不能大于Int32.MaxValue的九分之一</param>
    /// <returns>进行乘法运算后的乘法类</returns>
    public static Multiplication operator *(Multiplication multiplication, int multiplier)
    {
      return multiplication.Multiply(multiplier);
    }
    /// <summary>
    /// 将指定的被乘数隐式转换为乘法类
    /// </summary>
    /// <param name="multiplicand">被乘数</param>
    /// <returns>转换后的乘法类</returns>
    public static implicit operator Multiplication(int multiplicand)
    {
      return new Multiplication(multiplicand);
    }
    /// <summary>
    /// 将乘法类显式转换为int
    /// </summary>
    /// <param name="multiplication">乘法类</param>
    /// <returns>转换后的int</returns>
    public static explicit operator int(Multiplication multiplication)
    {
      int value = 0;
      int digit = 1;
      var result = multiplication._result;
      for (int i = result.Length - 1; i > multiplication._topDigit - 1; i--)
      {
        value += result[i] * digit;
        digit *= 10;
      }
      return value;
    }
    #endregion Operators
    /// <summary>
    /// 与指定的乘数进行乘法运算
    /// </summary>
    /// <param name="multiplier">乘数,不能大于Int32.MaxValue的十分之一</param>
    /// <returns>进行乘法运算后的乘法类</returns>
    public Multiplication Multiply(int multiplier)
    {
      Contract.Assert(MaxMultiplier > multiplier);
      int digit = GetDigits(multiplier);
      //加上被乘数的位数
      for (int i = _topDigit; i < _result.Length; i++)
      {
        int d = GetDigits(_result[i]);
        d += _result.Length - i - 1; //加上权的位数，比如100对应2位，1000对应3位
        digit += d;
      }
      //扩宽一位,容纳权值
      digit += 1;
      //位数不够，开始重新分配结果数组
      if (digit > _result.Length)
      {
        var result = new int[digit];
        //有效数字长度
        int validLength = _result.Length - _topDigit;
        Array.Copy(_result, _topDigit, result, result.Length - validLength, validLength);
        _topDigit += digit - _result.Length;
        _result = result;
      }
      //进行运算
      for (int i = _topDigit; i < _result.Length; i++)
      {
        _result[i] *= multiplier;
      }
      Carry();
      return this;
    }
    #endregion Public Methods
    #region Private Methods
    /// <summary>
    /// 进位
    /// </summary>
    private void Carry()
    {
      //从被乘数个数到最高位的前一位,依次进位
      for (int i = _result.Length - 1; i > _topDigit - 1; i--)
      {
        int carry = _result[i] / 10;
        _result[i] = _result[i] % 10;
        _result[i - 1] += carry;
      }
      //在被乘数的最高位进位
      for (int i = _topDigit - 1; ; i--)
      {
        int carry = _result[i] / 10;
        _result[i] = _result[i] % 10;
        if (0 != carry)
        {
          _result[i - 1] += carry;
        }
        else
        {
          break;
        }
      }
      UpdateTopDigit();
    }
    /// <summary>
    /// 获取数字的位数
    /// </summary>
    /// <param name="number">数字</param>
    /// <returns>位数</returns>
    private int GetDigits(int number)
    {
      return (int)Math.Ceiling(Math.Log10(number));
    }
    /// <summary>
    /// 更新最高位
    /// </summary>
    private void UpdateTopDigit()
    {
      _topDigit = 0;
      for (int i = 0; i < _result.Length; i++)
      {
        if (_result[i] != 0)
        {
          _topDigit = i;
          break;
        }
      }
    }
    #endregion Private Methods
  }

使用方法也很简单：

/// <summary>
    /// 计算阶乘
    /// </summary>
    /// <param name="n">要计算的阶乘</param>
    /// <returns>阶乘的结果，数字从高位到低位</returns>
    static IEnumerable<int> Factrial(int n)
    {
      var mul = new Multiplication();
      for (int i = 2; i <= n; i++)
      {
        mul *= i;
      }
      return mul.Result;
    }

扩展正如上面所说，只能计算不超过int.MaxValue九分之一的阶乘，如果需要计算更大的阶乘，就不能再直接将乘数的每位与被乘数相乘，而是需要进一步的细化，将乘数的每位依次与被乘数的每位相乘求和。例如：11x11=10*11+1*11=（10*10+10*1）+（1*10+1*1）。在此就不提供代码实现了。
同样的思路，也可将除法化为减法。
BigInteger 结构上面说了那么多，然并卵。从.Net Framework 4.0开始，就提供了BigInteger结构，代表一个任意大的整数，其值在理论上已没有上部或下部的界限。在此就不细谈了，具体可参考BigInteger结构。
参考资料《程序员的数学思维修炼》

[C++] 阶乘的增长和解决方案

相关帖子

iOS全埋点解决方案-数据同步

iOS全埋点解决方案-采集奔溃

iOS全埋点解决方案-APP和H5打通

CADisplayLink、NSTimer循环引用解决方案

0基础入门Android端实时聊天

Ubuntu20.04出现段错误核心已转储问题解决方案

XSLT – 服务器端概述

什么是IDE（集成开发环境）？

落地DevOps，探索高效研发运营一体化解决方案

学到就是赚到，面试加分项之WebServer线程池管理！

Green LV4