概述感知机分类一文中提到了感知机模型在分类问题上的应用,如果,我们需要将其使用于回归问题呢,应该怎样处理呢?
其实只要修改算法的最后一步,
sign(x)={+1−1,x≥0,x<0(1.1)sign(x)={+1,x≥0−1,x<0(1.1) sign(x)=\left\{\begin{matrix}+1 &, x\geq 0\\ -1 &, x< 0\end{matrix}\right.\tag{1.1}sign(x)={+1−1,x≥0,x<0(1.1)
函数即可。经过sign函数的处理,只可能是两个值,要么1,要么-1,。如果将最后的sign函数改成该函数:
f(x)=x(1.2)f(x)=x(1.2) f(x)=x\tag{1.2}f(x)=x(1.2)
那么,最后的输出值就是一个实数而不是1或-1中的一个值了,这样就达到了回归的目的。
损失函数在实际问题中,损失函数是根据不同的问题进行设计的,因此,单单改变了激活函数还不够,还需要改变损失函数,通常情况下,回归问题使用的损失函数为:
e=12(y−yˆ)2(2.1)e=12(y−y^)2(2.1) e=\frac{1}{2}(y-\hat{y})^2\tag{2.1}e=21(y−y^)2(2.1)
在公式(2.1)中,yy yy表示训练样本里面的标记,也就是实际值;yˆy^ \hat{y}y^表示模型计算的出来的预测值。ee ee叫做单个样本的误差。至于为什么前面要乘1/21/2 1/21/2,是为了后面计算方便。
根据公式(2.1),在nn nn个样本的数据集中,可以将总误差EE EE记为:
E=12∑i=1n(y(i)−yˆ(i))2(2.2)E=12∑i=1n(y(i)−y^(i))2(2.2) \begin{aligned}E&=\frac{1}{2}\sum_{i=1}^{n}(y^{(i)}-\hat{y}^{(i)})^2\end{aligned}\tag{2.2}E=21i=1∑n(y(i)−y^(i))2(2.2)
在公式(2.2)中,y(i)y(i) y^{(i)}y(i)表示第ii ii个样本的真实值,yˆ(i)y^(i) \hat{y}^{(i)}y^(i)表示第ii ii个样本的预测值。且
yˆ(i)=h(x(i))=wTx(i)(2.3)y^(i)=h(x(i))=wTx(i)(2.3) \begin{aligned}\hat{y}^{(i)}&=h(\mathrm{x}^{(i)})\\&=\mathrm{w}^T\mathrm{x^{(i)}}\end{aligned}\tag{2.3}y^(i)=h(x(i))=wTx(i)(2.3)
我们的目的,是训练模型:求取到合适的ww \mathrm{w}w,使(2.2)取得最小值。
求参数的方法
3.1 极大似然估计
该方法之前有提到过,大致思路为让损失函数对参数求导并令其为0,求出参数的值。具体的可以参考线性回归模型 ,但该方法仅适用于激活函数为f(x)=xf(x)=x f(x)=xf(x)=x的情况。
3.2 梯度下降算法
该方法是计算机通过强大的计算能力,一步步把极值点“试”出来,大致过程如下:
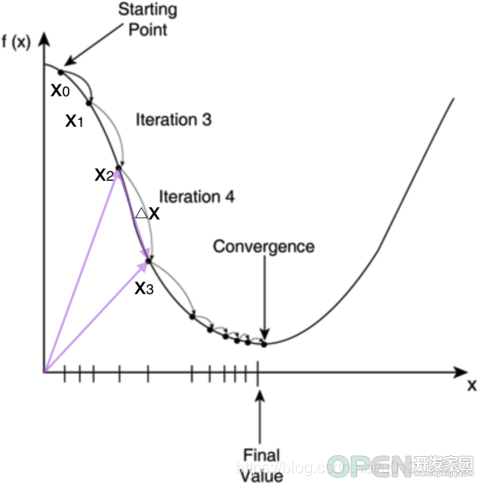
还记的感知机学习的步骤吗?主要是解决两个问题:
首先随机选择一个点xx xx,在之后的过程中每次修改该点,经过数次迭代之后最终到达函数的最小值点。根据梯度的性质:梯度的反方向是函数值下降最快的方向,每次沿着梯度相反的方向修改xx xx的值,最后是有可能走到极小值附近的。该公式可以表示为:
xnew=xold−η∇f(x)(3.1)xnew=xold−η∇f(x)(3.1) \mathrm{x}_{new}=\mathrm{x}_{old}-\eta\nabla{f(x)}\tag{3.1}xnew=xold−η∇f(x)(3.1)
将其应用于我们的目标函数的权值中时,则有
wnew=wold−η∇E(w)(3.2)wnew=wold−η∇E(w)(3.2) \begin{aligned}\mathrm{w}_{new}=&\mathrm{w}_{old}-\eta\nabla{E(\mathrm{w})}\\\tag{3.2}\end{aligned}wnew=wold−η∇E(w)(3.2)
对∇E(w)∇E(w) \nabla{E(\mathrm{w})}∇E(w)则有:
∇E(w)=∂∂wE(w)=∂∂w12∑i=1n(y(i)−yˆ(i))2=12∂∂w∑i=1n(y(i)2−2yˆ(i)y(i)+yˆ(i)2)=12∂∂w∑i=1n(−2yˆ(i)y(i)+yˆ(i)2)=12∑i=1n[−2y(i)∂yˆ(i)∂w+∂yˆ(i)2∂w]=12∑i=1n[−2y(i)∂wTx(i)∂w+2yˆ(i)∂wTx(i)∂w]=12∑i=1n[−2y(i)x(i)+2yˆ(i)x(i)]=−∑i=1n(y(i)−yˆ(i))x(3.3)∇E(w)=∂∂wE(w)=∂∂w12∑i=1n(y(i)−y^(i))2=12∂∂w∑i=1n(y(i)2−2y^(i)y(i)+y^(i)2)=12∂∂w∑i=1n(−2y^(i)y(i)+y^(i)2)=12∑i=1n[−2y(i)∂y^(i)∂w+∂y^(i)2∂w]=12∑i=1n[−2y(i)∂wTx(i)∂w+2y^(i)∂wTx(i)∂w]=12∑i=1n[−2y(i)x(i)+2y^(i)x(i)]=−∑i=1n(y(i)−y^(i))x(3.3) \begin{aligned}\nabla{E(\mathrm{w})}&=\frac{\partial}{\partial\mathrm{w}}E(\mathrm{w})\\&=\frac{\partial}{\partial\mathrm{w}}\frac{1}{2}\sum_{i=1}^{n}(y^{(i)}-\hat{y}^{(i)})^2\\&=\frac{1}{2}\frac{\partial}{\partial\mathrm{w}}\sum_{i=1}^{n}(y^{(i)2}-2\hat{y}^{(i)}y^{(i)}+\hat{y}^{(i)2})\\&=\frac{1}{2}\frac{\partial}{\partial\mathrm{w}}\sum_{i=1}^{n}(-2\hat{y}^{(i)}y^{(i)}+\hat{y}^{(i)2})\\&=\frac{1}{2}\sum_{i=1}^{n}[-2y^{(i)}\frac{\partial \hat{y}^{(i)}}{\partial\mathrm{w}}+\frac{\partial \hat{y}^{(i)2}}{\partial \mathrm{w}}]\\&=\frac{1}{2}\sum_{i=1}^{n}[-2y^{(i)}\frac{\partial \mathrm{w}^T\mathrm{x^{(i)}}}{\partial\mathrm{w}}+2\hat{y}^{(i)}\frac{\partial \mathrm{w}^T\mathrm{x^{(i)}}}{\partial \mathrm{w}}]\\&=\frac{1}{2}\sum_{i=1}^{n}[-2y^{(i)}\mathrm{x^{(i)}}+2\hat{y}^{(i)}\mathrm{x^{(i)}}]\\&=-\sum_{i=1}^{n}(y^{(i)}-\hat{y}^{(i)})\mathrm{x}\tag{3.3}\end{aligned}∇E(w)=∂w∂E(w)=∂w∂21i=1∑n(y(i)−y^(i))2=21∂w∂i=1∑n(y(i)2−2y^(i)y(i)+y^(i)2)=21∂w∂i=1∑n(−2y^(i)y(i)+y^(i)2)=21i=1∑n[−2y(i)∂w∂y^(i)+∂w∂y^(i)2]=21i=1∑n[−2y(i)∂w∂wTx(i)+2y^(i)∂w∂wTx(i)]=21i=1∑n[−2y(i)x(i)+2y^(i)x(i)]=−i=1∑n(y(i)−y^(i))x(3.3)
所以,梯度更新公式为:
wnew=wold+η∑ni=1(y(i)−yˆ(i))x(i)(3.4)wnew=wold+η∑i=1n(y(i)−y^(i))x(i)(3.4) \mathrm{w}_{new}=\mathrm{w}_{old}+\eta\sum_{i=1}^{n}(y^{(i)}-\hat{y}^{(i)})\mathrm{x}^{(i)}\tag{3.4}wnew=wold+ηi=1∑n(y(i)−y^(i))x(i)(3.4)
若有M+1个特征,(常数项也包括在内),则w,xw,x \mathrm{w},\mathrm{x}w,x是M+1维列向量,所以(3.4)可以写成
⎡⎣⎢⎢⎢⎢w0w1w2...wm⎤⎦⎥⎥⎥⎥new=⎡⎣⎢⎢⎢⎢w0w1w2...wm⎤⎦⎥⎥⎥⎥old+η∑ni=1(y(i)−yˆ(i))⎡⎣⎢⎢⎢⎢⎢⎢1x(i)1x(i)2...x(i)m⎤⎦⎥⎥⎥⎥⎥⎥[w0w1w2...wm]new=[w0w1w2...wm]old+η∑i=1n(y(i)−y^(i))[1x1(i)x2(i)...xm(i)] \begin{bmatrix}w_0 \\w_1 \\w_2 \\... \\w_m \\\end{bmatrix}_{new}=\begin{bmatrix}w_0 \\w_1 \\w_2 \\... \\w_m \\\end{bmatrix}_{old}+\eta\sum_{i=1}^{n}(y^{(i)}-\hat{y}^{(i)})\begin{bmatrix}1 \\x_1^{(i)} \\x_2^{(i)} \\... \\x_m^{(i)} \\\end{bmatrix}⎣⎢⎢⎢⎢⎡w0w1w2...wm⎦⎥⎥⎥⎥⎤new=⎣⎢⎢⎢⎢⎡w0w1w2...wm⎦⎥⎥⎥⎥⎤old+ηi=1∑n(y(i)−y^(i))⎣⎢⎢⎢⎢⎢⎡1x1(i)x2(i)...xm(i)⎦⎥⎥⎥⎥⎥⎤
与分类器的比较
算法分类回归模型sign(x)={+1−1,x≥0,x<0sign(x)={+1,x≥0−1,x<0 sign(x)=\left\{\begin{matrix}+1 &, x\geq 0\\ -1 &, x< 0\end{matrix}\right.sign(x)={+1−1,x≥0,x<0f(x)=xf(x)=x f(x)=xf(x)=x训练规则w←w+η(y−yˆ)xw←w+η(y−y^)x \mathrm{w}\gets\mathrm{w}+\eta(y-\hat{y})\mathrm{x}w←w+η(y−y^)xw←w+η(y−yˆ)xw←w+η(y−y^)x \mathrm{w}\gets\mathrm{w}+\eta(y-\hat{y})\mathrm{x}w←w+η(y−y^)x
5.代码实现代码在这里, 翻我牌子
制作数据import numpy as np
from sklearn.model_selection import train_test_split
def load_data(n):
X = np.arange(0, 10, 0.1)
y = X + (np.random.rand(len(X)) - 0.5) * n
X_train, X_test, y_train, y_test = train_test_split(X, y)
return X_train, X_test, y_train, y_test
def show_data():
import matplotlib.pyplot as plt
print(X.shape)
plt.scatter(X, y)
plt.plot(X, X)
plt.show()
主代码'''
用感知机实现回归算法
'''
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
class ProceptronRegression():
def init(self, max_itr=100, lr_rate=0.01, eps=0.1):
self.max_itr = max_itr
self.lr_rate = lr_rate
self.eps = epsdef SquareLoss(self, y, y_pred):
return np.sum((y - y_pred)**2) / len(y)**2
def fit(self, X, y):
w = np.random.rand(2) # b, a, 构造y = a*x + b
for itr in range(self.max_itr):
# print(len(X)**2)
temp = 0
for d in range(len(X)):
x_ = np.array([1, X[d]])
y_ = y[d]
temp += (y_ - np.dot(w, x_)) * x_
# print(temp)
w += self.lr_rate * temp
# print(w)
self.w = w
y_pred = self.predict(X)
if self.SquareLoss(y, y_pred) < self.eps:
print("iterations:", itr+1)
break
print("Train Finished !")
return
def predict(self, X):
return np.dot(X, self.w[1]) + self.w[0]
def score(self, X, y):
y_pred = self.predict(X)
return self.SquareLoss(y, y_pred)
if name == "main":
from Data.make_regression import load_data
X_train, X_test, y_train, y_test = load_data(4) # 参数为离散程度
rgs = ProceptronRegression(max_itr=100, lr_rate=1e-4, eps=0.01)
rgs.fit(X_train, y_train)
print("training loss: ", rgs.score(X_test, y_test))y_pred = rgs.predict(X_test)
print("predict: ", y_pred)
plt.scatter(X_train, y_train, label="train")
xx = np.arange(X_train.min(), X_train.max(), 0.01)
plt.plot(xx, rgs.w[1]*xx + rgs.w[0], 'r')
plt.scatter(X_test, y_pred, label='predict')
plt.legend()
plt.show()
</div>
|

![]() 编程语言
发布于:2021-08-09 15:58
|
阅读数:597
|
评论:0
编程语言
发布于:2021-08-09 15:58
|
阅读数:597
|
评论:0


 QQ好友和群
QQ好友和群 QQ空间
QQ空间