抛物样条曲线的原理说明及画抛物曲线的一个类

三叶草

朱金灿              
假如我们采用矢量表达式来表示参数化的二次曲线，那么可以把抛物线的表达式写成如下的一般形式：
P(t)=A1+ A2t+ A3t2      (0=<t<=1)


该抛物线过P1, P2, P3三个点，并且：
1.       抛物线以P1点为始点。当参变量t=0时，曲线过P1点；
2.       抛物线以P3点为终点。当参变量t=0时，曲线过P3点；
3.       当参变量t=0.5时，曲线过P2点,且切矢量等于P3—P1。


t=0: P(0)= A1= P1
t=1: P(1)= A1 + A2+ A3=P3     
t=0.5:P(0.5)= A1 + 0.5A2+0.25 A3=P2     
通过解联立方程，得到三个参数A1 、 A2、 A3分别为：
A1 = P1     
A2=4 P2—P3—3P1
A3=2P1+2P3—4P2     


把求出的这三个系数的值，代入抛物线的表达式P(t)=A1+ A2t+ A3t2     
得：P(t)=（2t—3t+1）P1 +(4t—4t2)P2+(4t2—t)P3   (0=<t<=1)


设有一离散型值点列Pi（i=1,2,……,n）,每经过相邻三点作一段抛物线，由于有n个型值点，所以可以做n-2条抛物线段。
在这n—2条抛物线段中，第i条抛物线段为经过Pi, Pi+1, Pi+2三点，所以它的表达式应为：Si(ti)=（2t2i—3ti+1）Pi +(4 ti—4 t2i) Pi+1 +(2t2i—ti) Pi+2     (0=< ti <=1)


同理，第i+1条抛物线段为经过Pi+1, Pi+2, Pi+3三点，所以它的表达式应为：Si+1(ti+1)=（2t2i+1—3ti+1+1）Pi+1 +(4 ti+1—4 t2i+1) Pi+2 +(2t2i+1—ti+1) Pi+3     (0=< ti+1 <=1)
一般来说，每两段曲线之间的搭接区间，两条抛物线是不可能重合的。如下图所示：

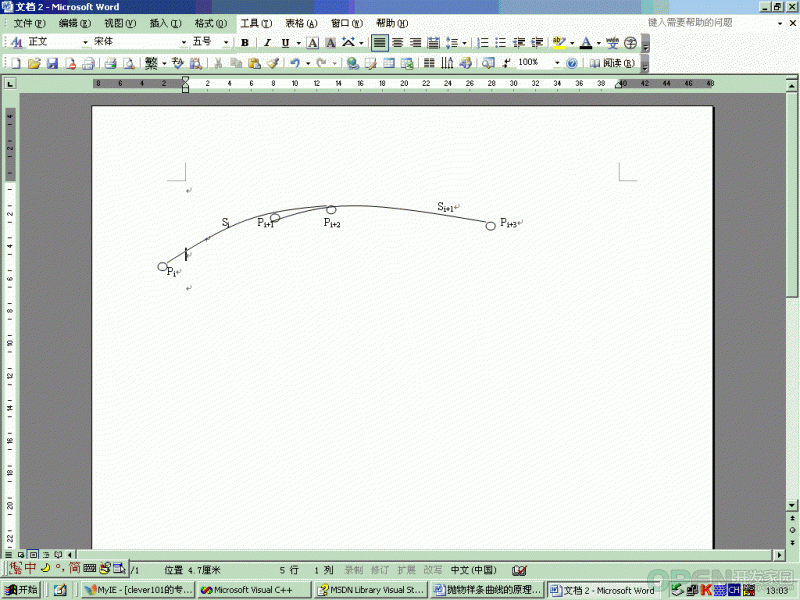
显然，对于拟合曲线来说，整个型值点必须只能用一条光滑的曲线连接起来。为了做到这一点，必须找一种方法把Si和Si+1 这样的曲线段的共同区间结合起来。这种方法就是加权合成方法。
我们设共同区间的函数是Pi+1(t)=f (T ) Si(ti)+g ( T) Si+1(ti+1). 其中f (T ) 和 g ( T) 是权函数。在抛物样条曲线中我们取简单的一次函数为权函数，且具有互补性，设
f (T ) =1—T
g ( T) =T
这样Pi+1(t)= (1—T ) Si(ti)+ T Si+1(ti+1).因为 函数中有T、ti和ti+1三个参数，因此接下来我们的工作是统一参数。我们可以三个参变量统一形式为：
T=2t
ti=0.5+t
ti+1=t


这样Pi+1(t)= （—2t3+4t2—t）Pi +(12t3—410t2+1) Pi+1 +(—12t3+8t2+t) Pi+2 +(4t3—2t2) Pi+3     (0=< ti <=0.5)


从几何意义上说，函数Pi+1(t)表示的上图的点Pi+1,到Pi+2 之间的线段。但是我们应该看到这种方法从n个点中只能得到n—3段曲线。但是n个型值点应有n—1段曲线。一个直接的想法是添加两个辅助点。那么如何添加呢？
方法一：两个辅助点为P0和Pn+1,  P0=P1，Pn+1= Pn ,这样画出的曲线为一条不闭合的自由曲线。
方法二：添加三个辅助点，P0、Pn+1和Pn+2，然后P0=Pn，Pn+1= P1, ，Pn+2= P2,这样画出的曲线为一条闭合的曲线。


下面介绍根据上面原理而设计的一个画抛物曲线的一个类：
class CParspl : public CObject 
{
DECLARE_SERIAL(CParspl)
public:
CParspl(int nLineStyle,int nLineWidth, COLORREF crLineColor);
virtual ~CParspl();
void SetPoint(const CPoint &point);   // 添加坐标点
void DrawFreeLine(CDC *pDC);//  画自由端抛物曲线
void DrawCloseLine(CDC *pDC); // 画封闭端抛物曲线
void Serialize(CArchive & ar);
protected:
CParspl();
/*public attributes*/
public:
int m_bIsFreeLine;
/*private attibutes*/
private:
CArray<CPoint,CPoint> ParsplPoint;  // 定义插值点数组
COLORREF m_crLineColor;  // 定义线色
int  m_nLineStyle;      // 定义线型
int  m_nLineWidth;      //定义线宽
};






const int  Clip=10;






CParspl::CParspl()  // 默认的构造函数
{


}


CParspl::~CParspl()
{


}


CParspl::CParspl(int nLineStyle,int nLineWidth, COLORREF crLineColor)
{
m_nLineStyle = nLineStyle;
m_nLineWidth = nLineWidth;
m_crLineColor = crLineColor;
ParsplPoint.Add(CPoint(0,0));   //初始化第一个点
m_bIsFreeLine = 1;
}


void CParspl::SetPoint(const CPoint &point)
{
ParsplPoint.Add(point);
}


void CParspl::DrawFreeLine(CDC *pDC)
{
if(ParsplPoint.GetSize() < 4) return;
CPen LinePen(m_nLineStyle,m_nLineWidth,m_crLineColor);
int i=0,j=0;
int n=0;
n=ParsplPoint.GetSize();
double t1,t2,t3,t,a,b,c,d,x,y;
ParsplPoint[0].x=ParsplPoint[1].x;
ParsplPoint[0].y=ParsplPoint[1].y;
CPoint pt=ParsplPoint.GetAt(n-1);
ParsplPoint.Add(pt);
t=             0.5f      /Clip;
CPen *pLinePen=pDC->SelectObject(&LinePen);
pDC->MoveTo(ParsplPoint[1].x,ParsplPoint[1].y);
for (i=0;i<n-2;i++)
{
for(j=1;j<Clip;j++)
{
t1=j*t;
t2=t1*t1;
t3=t2*t1;
a=4.0*t2-t1-4.0*t3;
b=1.0-10.0*t2+12.0*t3;
c=t1+8.0*t2-12.0*t3;
d=4.0*t3-2.0*t2;
x=a*ParsplPoint.x+b*ParsplPoint[i+1].x+c*ParsplPoint[i+2].x+d*ParsplPoint[i+3].x;
y=a*ParsplPoint.y+b*ParsplPoint[i+1].y+c*ParsplPoint[i+2].y+d*ParsplPoint[i+3].y;
pDC->LineTo(int(x),int(y));
}
pDC->LineTo(ParsplPoint[i+2].x,ParsplPoint[i+2].y);
}
for(i=0;i<n;i++)
{
pt=ParsplPoint.GetAt(i);
pDC->Ellipse(pt.x-2,pt.y-2,pt.x+2,pt.y+2);
}
/*        将旧画笔选回设备环境*/
pDC->SelectObject(pLinePen);
/*删除辅助点*/   ParsplPoint.RemoveAt(ParsplPoint.GetUpperBound());


}


void CParspl::DrawCloseLine(CDC *pDC)
{
if(ParsplPoint.GetSize() < 4) return;
CPen LinePen(m_nLineStyle,m_nLineWidth,m_crLineColor);
int i=0,j=0;
int n=0;
n=ParsplPoint.GetSize();
double t1,t2,t3,t,a,b,c,d,x,y;
ParsplPoint[0].x=ParsplPoint[n-1].x;
ParsplPoint[0].y=ParsplPoint[n-1].y;
CPoint pt=ParsplPoint.GetAt(1);
ParsplPoint.Add(pt);
pt=ParsplPoint.GetAt(2);
ParsplPoint.Add(pt);
t=             0.5f      /Clip;
CPen *pLinePen=pDC->SelectObject(&LinePen);
pDC->MoveTo(ParsplPoint[1].x,ParsplPoint[1].y);
for (i=0;i<n-1;i++)
{
for(j=1;j<Clip;j++)
{
t1=j*t;
t2=t1*t1;
t3=t2*t1;
a=4.0*t2-t1-4.0*t3;
b=1.0-10.0*t2+12.0*t3;
c=t1+8.0*t2-12.0*t3;
d=4.0*t3-2.0*t2;
x=a*ParsplPoint.x+b*ParsplPoint[i+1].x+c*ParsplPoint[i+2].x+d*ParsplPoint[i+3].x;
y=a*ParsplPoint.y+b*ParsplPoint[i+1].y+c*ParsplPoint[i+2].y+d*ParsplPoint[i+3].y;
pDC->LineTo(int(x),int(y));
}
pDC->LineTo(ParsplPoint[i+2].x,ParsplPoint[i+2].y);
}
for(i=0;i<n;i++)
{
pt=ParsplPoint.GetAt(i);
pDC->Ellipse(pt.x-2,pt.y-2,pt.x+2,pt.y+2);
}
/*将旧画笔选回设备环境*/
pDC->SelectObject(pLinePen);
/*删除最后两个辅助点*/
ParsplPoint.RemoveAt(ParsplPoint.GetUpperBound());
ParsplPoint.RemoveAt(ParsplPoint.GetUpperBound());
}


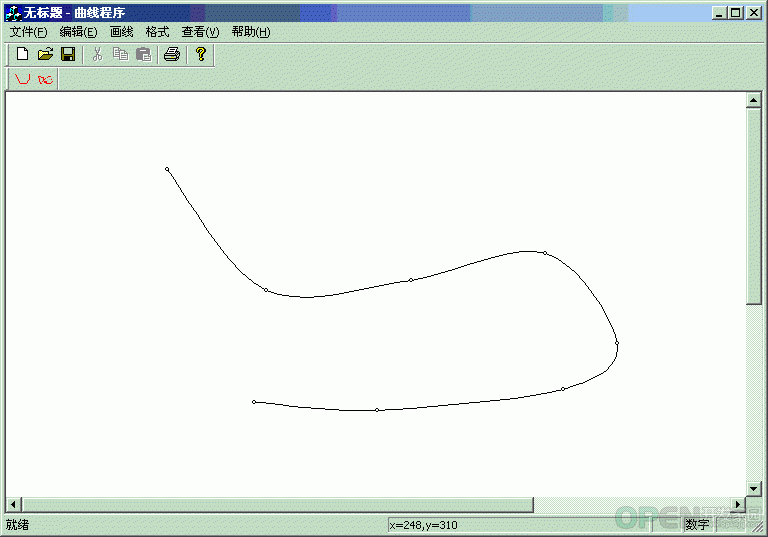
程序效果图：
自由端曲线：

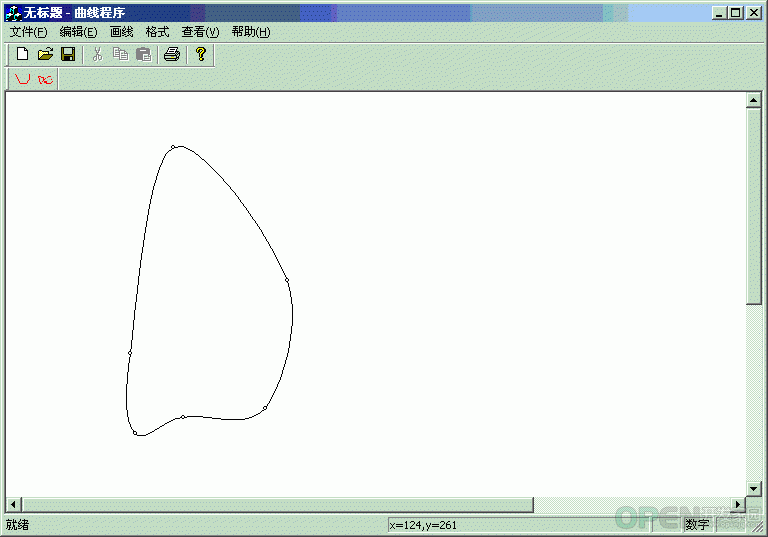
封闭端曲线：