Java中关于二叉树的概念以及搜索二叉树详解

小蚂蚁

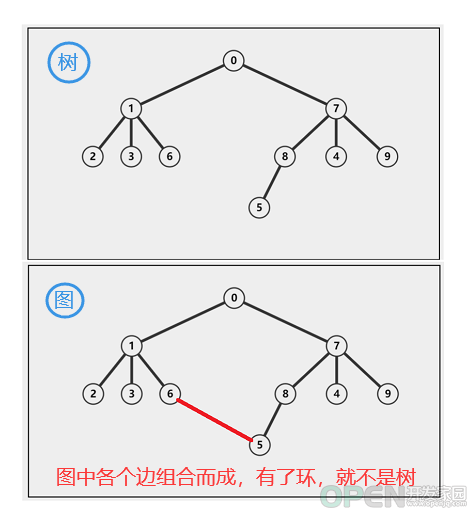
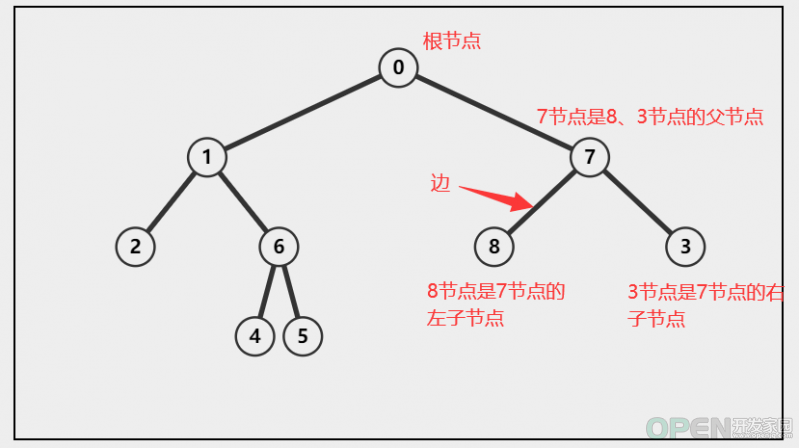
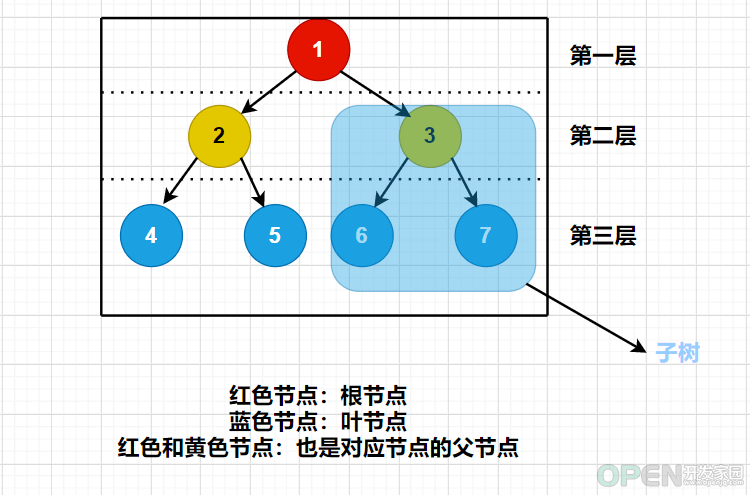
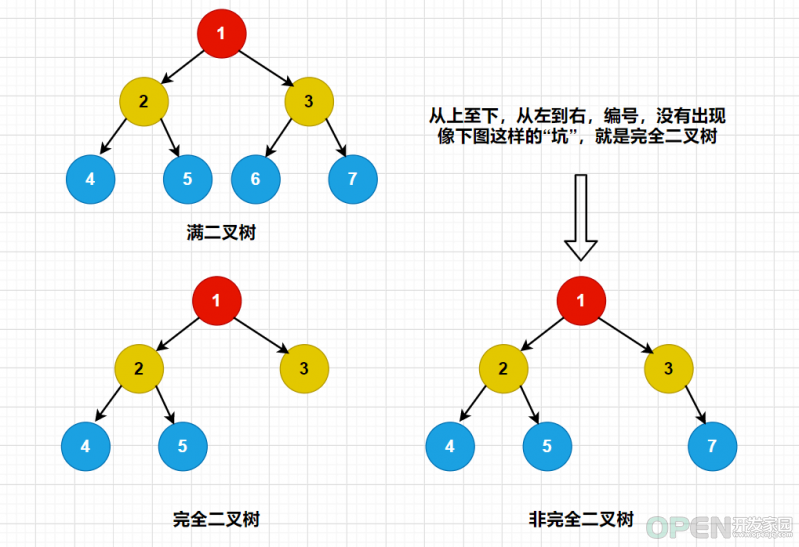
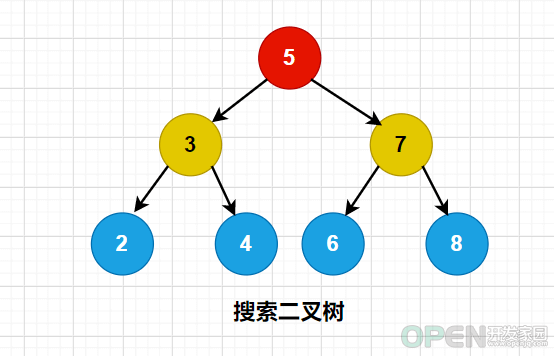
二叉树是一种很有用的非线性结构,日常的开发中常会用到，关于二叉树的概念以及搜索二叉树本文给大家介绍的非常详细，对大家的学习或工作具有一定的参考借鉴价值，需要的朋友可以参考下
hello, everyone. Long time no see. 本期文章，我们主要讲解一下二叉树的相关概念，顺便也把搜索二叉树（也叫二叉排序树）讲一下。我们直接进入正题吧！GitHub源码链接

一、二叉树的概念

为什么要使用二叉树？
为什么要用到树呢?因为它通常结合了另外两种数据结构的优点:一种是有序数组，另一种是链表。在树中查找数据项的速度和在有序数组中查找一样快，并且插入数据项和删除数据项的速度也和链表一样。下面，我们先来稍微思考一下这些话题，然后再深入地研究树的细节。
在有序数组中插入数据太慢了，而在链表中查找数据也太慢了。所以到后来就有了二叉树这种数据结构。

树是什么？
在深入讲解二叉树前，我们先简单地认识一下树这个概念。树是由若干个节点和边组合而成，例如，可以把城市看成节点，将各个城市之间的交通路线看成边。当然说的更准确一点，这个例子更应该是属于图的范畴内，关于图的相关知识点。我们到后面再来讨论。如下图，就是一棵树。

树的相关术语！
​ 如下图所示

根节点
​ 树最顶端的节点称为根节点，一棵树只有一个根节点，一般也是整棵树遍历的开始。

路径
​ 设想一下，从树中的一个节点，沿着边走向另一个节点，所经过的节点顺序排列就称为“路径”。

父节点
​ 就像这个名称一样，在二叉树中扮演“父亲”的角色， 在二叉树中的每一个节点（除了根节点），都有一个边向上可以找到该节点的”父节点“。

子节点
​ 每个节点都可能有一条或多条边向下连接其他节点，下面的这些节点就称为它的“子节点”。

叶节点
​ 没有子节点的节点称为“叶子节点”或简称“叶节点”。树中只有一个根，但是可以有很多叶节点。

子树
​ 每个节点都可以作为“子树”的根，它和它所有的子节点，子节点的子节点等都含在子树中。就像家族中那样，一个节点的子树包含它所有的子孙。

访问
​ 当程序控制流程到达某个节点时，就称为“访问”这个节点，通常是为了在这个节点处执行某种操作，例如查看节点某个数据字段的值或显示节点。如果仅仅是在路径上从某个节点到另一个节点时经过了一个节点，不认为是访问了这个节点。

层（深度）
​ 也就相当于我们人一样，我们这一辈人，就可以看做一层。而爸妈那一辈，又是另外一层。

关键字
​ 如图中所示，每个节点里，有一个数值，这个数值我们就称为关键字。

满二叉树
​ 在一颗二叉树中，如果所有分支节点都存在左子树和右子树，并且所有的叶节点都在同一层上，这样的二叉树，称为满二叉树。如上图所示。

完全二叉树
​ 对一颗具有n个节点的二叉树按从上至下，从左到右的顺序编号，如果编号为i(1 <= i <= n)的节点与同样深度的满二叉树中编号为i的节点在二叉树中的位置完全一样，则这棵树就被称为完全二叉树。
从字面上的意思来看，满二叉树一定是完全二叉树，而完全二叉树不一定是满的。如下图：

二叉树的五大性质
1.在二叉树的第i层上，最多有2（i-1）的次方个节点。例如：第三层上，最多也就有4个节点。
2.深度为k的二叉树，最多有2k的次方 - 1个节点。 例如：深度为3的二叉树，最多也就只有7个节点。
3.对任何一颗二叉树，叶子节点的总数记为n0，度为2的节点的总数记为n2。则n0 = n2 + 1。解释：度为2的节点，指的是该节点左右子节点都有的情况，我们称为度为2的节点。那如果左右子节点，有且仅有一个的时候，我们就叫度为1的节点。
4.具有n个节点的完全二叉树的深度为 log2n + 1。（此处的对数 向下取整）
由满二叉树的定义我们可以知道，深度为k的 满二叉树的节点数n一定等于 2k的次方 - 1。因为这是最多的节点数，再由这个公式，我们就可以倒推出
k = log2(n + 1)。比如节点数为8的满二叉树，深度就是3。
5.如果对一颗有n个节点的完全二叉树的节点，按照从上至下，从左到右，对每一个节点进行编号：则有如下性质：
​ 1). 如果i=1，则该节点就是这棵树的根结点。若i不等于1，则i节点的父节点就是i / 2节点。
​ 2). 如果2i > n，(n为整棵树的总节点数)，则i节点没有左子节点，反之就是2i就是左子节点。
​ 3). 如果2i + 1 > n，(n为整棵树的总节点数)，则i节点没有右子节点，反之就是2i + 1就是右子节点。

二、搜索二叉树
上面我们讲解完了二叉树的一些基本的概念，现在我们继续来看下一个知识点：搜索二叉树。
定义：一个节点的左子节点的关键字值小于这个节点，右子节点的关键字值大于或等于这个父节点。如下图，就是一个搜索二叉树。

可能会有同学已经发现了一个规律，那就是搜索二叉树的中序遍历的结果就是一个升序的。所以在判断一颗树是不是搜索二叉树时，就可以从这里入手。
知道了定义，我们就可以根据定义来实现相应的代码。
节点结构

class TreeNode {
  int val; //关键字
  TreeNode left; //左子节点
  TreeNode right; //右子节点
  
  public TreeNode(int val) {
    this.val = val;
  }
}

搜索二叉树的整体框架结构

public class BST {
  private TreeNode root; //根结点
  
  public void insert(int val) { //插入新的节点
    
  }
  
  public void remove(int val) { //删除对应的节点
    
  }
  
  public boolean contains(int val) { //查询是否有该值
    
  }
}

我们就一个一个的讲解每一方法具体的实现：

插入
插入新的节点，这个算是比较简单的。我们拿到依次比较当前节点的值和传递进来的形参值，如果形参值更小一点，我们就往左子树上做递归，继续这个操作即可。

//递归解法
public void insert(int val) {
  root = process(val, root);
}

private TreeNode process(int val, TreeNode node) {
  if (node == null) { //如果当前节点为null，说明已经走到头了，此时创建节点，返回即可
    return new TreeNode(val);
  } 
  if (val < node.val) { //小于当前节点
    node.left = process(val, node.left);
  } else {
    node.right = process(val, node.right); //大于等于当前节点
  }
  return node;
}

//非递归解法
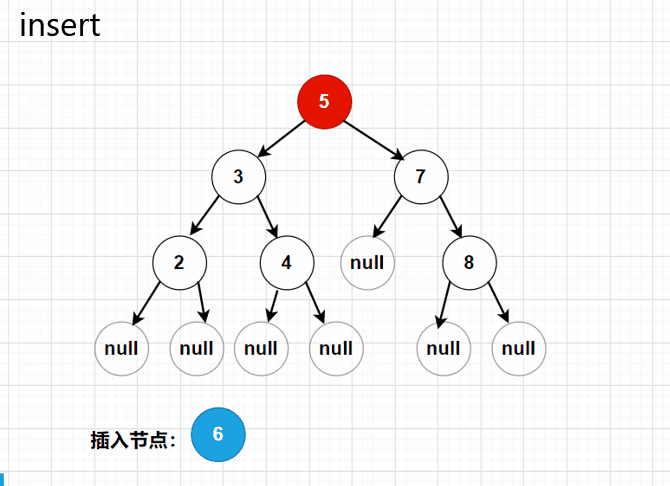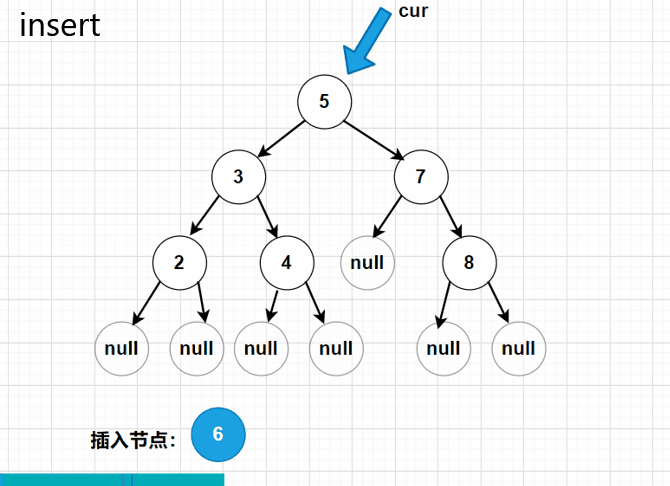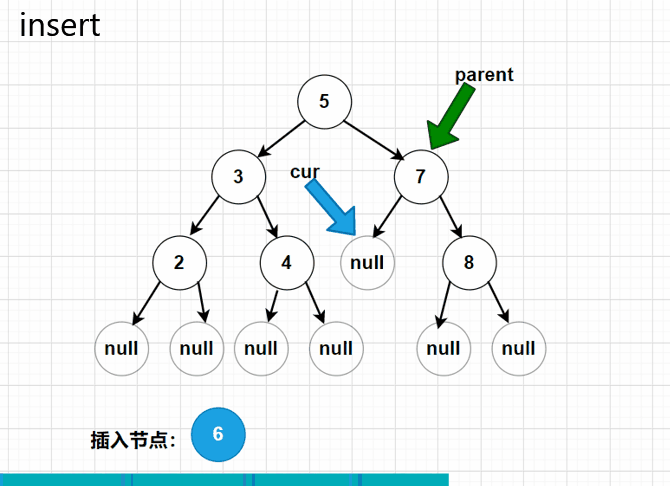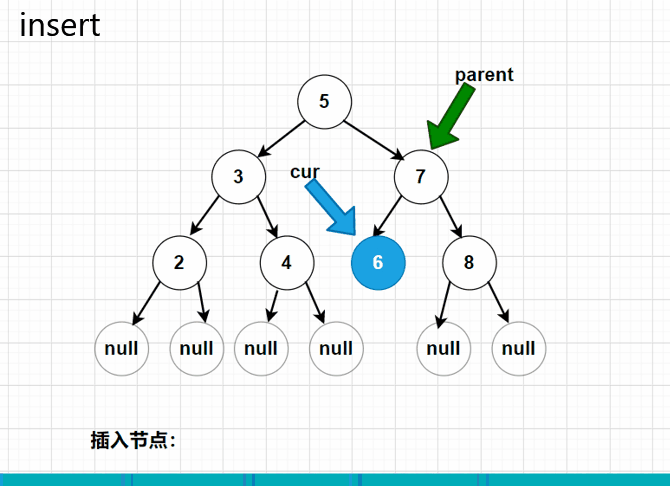
public void insert(int val) {
  TreeNode node = new TreeNode(val); //先创建好节点
  TreeNode parent = null; //父节点，用于连接新的节点
  TreeNode cur = root; //当前移动的节点
  
  if (root == null) {
    root = node; //还没有根结点的情况
  } else {
    while (true) {
      parent = cur;
      if (val < cur.val) { //小于当前节点的情况
        cur = cur.left;
        if (cur == null) { //如果为null了，说明走到了最后的节点
          parent.left = node;
          return;
        }
      } else { //大于当前节点的情况
        cur = cur.right;
        if (cur == null) {
          parent.right = node; //如果为null，就走到最后节点了
          return;
        }
      }
    }
  }
}

递归与非递归的解法，差异只是在于空间复杂度。当整棵树很大时，递归去调用，就会耗费大量的栈空间。而非递归的解法，只是耗费了几个引用的空间。

删除
删除是一个比较难的点，删除之后，还需要保持搜索二叉树的结构。所以我们需要分为三种情况：

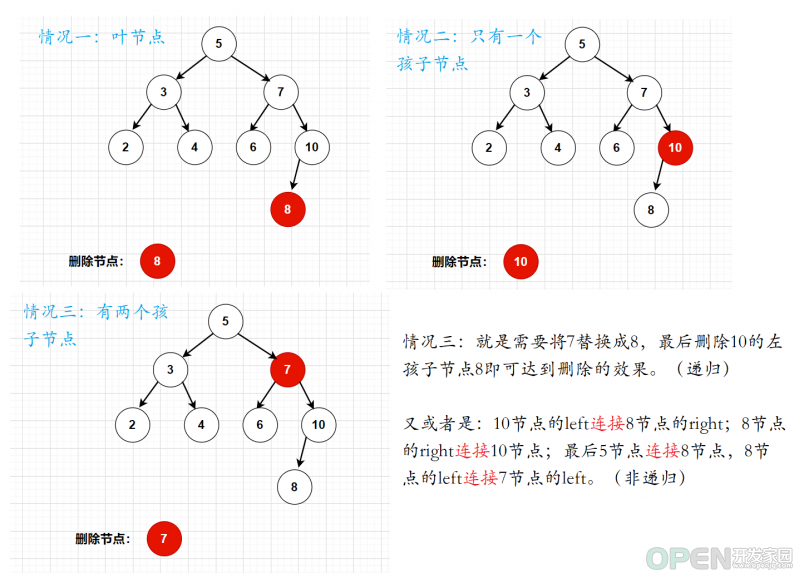
• 被删除节点是叶节点。
• 被删除节点只有一个孩子节点。
• 被删除节点有两个孩子节点。
  

我们需要循环遍历这颗树，找到需要被删除的节点，并且在遍历的过程中，还需要记录被删除节点的父节点是谁，以及被删除节点是父节点的左孩子还是右孩子。所以循环时，有三个变量，分别是parent、cur和isLeftChild。
在找到需要被删除的节点后。再对这个节点进行判断，看这个节点是叶节点？还是只有一个孩子节点？又或者是有两个孩子节点的情况。

• 如果是叶节点，parent的left（或者是right）置为null
• 如果只有一个节点，我们就需要绕过cur节点，直接连接cur的left或者right
• 如果是有两个节点，我们就需要找到cur的后继节点。也就是cur的右子树中，最小的节点。
  

其次我们还需要判断被删除的节点，是不是root根结点？如果是，就需要更换根结点。

非递归版本大致框架：

//非递归版本
public boolean remove(int val) { //删除对应的节点
  if (root == null) {
    throw new RuntimeException("root is null.");
  }

  TreeNode parent = root;
  TreeNode cur = root;
  boolean isLeftChild = true;

  while (cur != null && cur.val != val) { //循环查找需要被删除的节点
    parent = cur;
    if (val < cur.val) {
      cur = cur.left;
      isLeftChild = true;
    } else {
      cur = cur.right;
      isLeftChild = false;
    }
  }

  if (cur == null) { //没找到需要删除的节点
    return false;
  }

  //找到了需要被删除的节点
  if ( cur.left== null && cur.right == null) { //叶节点的情况
    if (cur == root) {
      root = null;
    } else if (isLeftChild) {
      parent.left = null;
    } else {
      parent.right = null;
    }
  } else if (cur.right == null) {
    if (cur == root) {
      root = root.left;
    } else if (isLeftChild) {
      parent.left = cur.left;
    } else {
      parent.right = cur.left;
    }
  } else if (cur.left == null) { //只有一个孩子节点的情况
    if (cur == root) {
      root = root.right;
    } else if (isLeftChild) {
      parent.left = cur.right;
    } else {
      parent.right = cur.right;
    }
  } else { //有两个孩子节点的情况
    TreeNode minNode = findMinNode(cur.right);
    if (cur == root) {
      root = minNode;
    } else if (isLeftChild) {
      parent.left = minNode;
    } else {
      parent.right = minNode;
    }
    minNode.left = cur.left; //新节点minNode的左孩子指向被删除节点cur的左孩子
    // C/C++语言，需要回收cur内存空间
  }
  return true;
}

private TreeNode findMinNode(TreeNode head)  {
  TreeNode pre = null;
  TreeNode cur = head;
  TreeNode next = head.left;
  while (next != null) {
    pre = cur;
    cur = next;
    next = next.left; //一直寻找该树的最左的节点
  }
  if (pre != null) {
    pre.left = cur.right; //cur就是最左边的节点，pre的cur的父节点。父节点的left指向cur的right
    cur.right = head; //cur的right指向head这个根结点
  }
  return cur; //返回最左边的节点
}

//递归版本
public void remove2(int val) {
  if (root == null) {
    throw new RuntimeException("root is null.");
  }

  process2(val, root);
}

private TreeNode process2(int val, TreeNode node) {
  if (node == null) {
    return null;
  }
  if (val < node.val) { //小于
    node.left = process2(val, node.left);
  } else if (val > node.val){ //大于
    node.right = process2(val, node.right);
  } else if (node.left != null && node.right != null) { //上面的if没成立，说明val相等。这里是两个孩子节点的情况
    
    node.val = getMinNodeVal(node.right); //覆盖右子树中最小的节点值
    
    node.right = process2(node.val, node.right); // 重新对已经覆盖的数值进行删除
    
  } else { //只有一个孩子节点或者没有节点的情况
    node = node.left != null? node.left : node.right;
  }
  return node;
}

private int getMinNodeVal(TreeNode node) {
  TreeNode pre = null;
  TreeNode cur = node;
  while (cur != null) {
    pre = cur;
    cur = cur.left;
  }
  return pre.val;
}

递归版本的删除，只是将右子树最小节点的值，赋值给了cur，然后递归调用去删除右子树上最小值的节点。
最后一个contains方法就简单了，遍历整颗二叉树，找到了val就返回true，否则返回false。

public boolean contains(int val) {
  TreeNode cur = root;
  while (cur != null) {
    if (cur.val == val) {
      return true;
    } else if (val < cur.val) {
      cur = cur.left;
    } else {
      cur = cur.right;
    }
  }
  return false;
}

最后自己再写一个中序遍历的方法，看看自己写的代码是否正确了呢。切记：搜索二叉树中序遍历的结果，一定是一个升序的。不知道怎么写遍历方法的，可以看一下前期文章：通俗易懂讲解C语言与Java中二叉树的三种非递归遍历方式。
好啦，本期文章就到此结束啦，我们下期见！！！
到此这篇关于Java中关于二叉树的概念以及搜索二叉树详解的文章就介绍到这了,更多相关Java 二叉树内容请搜索CodeAE代码之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持CodeAE代码之家！
原文链接：https://blog.csdn.net/x0919/article/details/119832187