特征工程个人笔记

• 1.概述
  

　　在工程实践中，我们得到的数据会存在有缺失值、重复值等，在使用之前需要进行数据预处理。数据预处理没有标准的流程，通常针对不同的任务和数据集属性的不同而不同。数据预处理的常用流程为：去除唯一属性、处理缺失值、属性编码、数据标准化正则化、特征选择、主成分分析。
　　2方法
　　2.1去除唯一性


　　唯一属性通常是一些id属性，这些属性并不能刻画样本自身的分布规律，所以简单地删除这些属性即可。
　　2.2处理缺失值


　　缺失值处理的三种方法：直接使用含有缺失值的特征；删除含有缺失值的特征（该方法在包含缺失值的属性含有大量缺失值而仅仅包含极少量有效值时是有效的）→dropna（）；缺失值补全→fillna( )。判断是否缺失→isnull( )
　　常见的缺失值补全方法：均值插补、同类均值插补、建模预测、高维映射、多重插补、极大似然估计、压缩感知和矩阵补全。
（1）均值插补　　如果样本属性的距离是可度量的，则使用该属性有效值的平均值来插补缺失的值；
（2）同类均值插补　　首先将样本进行分类，然后以该类中样本的均值来插补缺失值。
（3）建模预测　　将缺失的属性作为预测目标来预测，将数据集按照是否含有特定属性的缺失值分为两类，利用现有的机器学习算法对待预测数据集的缺失值进行预测。
　　该方法的根本的缺陷是如果其他属性和缺失属性无关，则预测的结果毫无意义；但是若预测结果相当准确，则说明这个缺失属性是没必要纳入数据集中的；一般的情况是介于两者之间。
（4）高维映射　　将属性映射到高维空间，采用独热码编码（one-hot）技术。将包含K个离散取值范围的属性值扩展为K+1个属性值，若该属性值缺失，则扩展后的第K+1个属性值置为1。
　　这种做法是最精确的做法，保留了所有的信息，也未添加任何额外信息，若预处理时把所有的变量都这样处理，会大大增加数据的维度。这样做的好处是完整保留了原始数据的全部信息、不用考虑缺失值；缺点是计算量大大提升，且只有在样本量非常大的时候效果才好。
（5）多重插补（MultipleImputation，MI）　　多重插补认为待插补的值是随机的，实践上通常是估计出待插补的值，再加上不同的噪声，形成多组可选插补值，根据某种选择依据，选取最合适的插补值。
（6）压缩感知和矩阵补全 （7）手动插补　　插补处理只是将未知值补以我们的主观估计值，不一定完全符合客观事实。在许多情况下，根据对所在领域的理解，手动对缺失值进行插补的效果会更好。
　　2.3 特征编码


　　2.3.1特征二元化

　　特征二元化的过程是将数值型的属性转换为布尔值的属性，设定一个阈值作为划分属性值为0和1的分隔点。
二进制转化-Binarizer


　　2.3.2独热编码（One-HotEncoding）

　　from sklearn.preprocessing import OneHotEncoder
独热编码采用N位状态寄存器来对N个可能的取值进行编码，每个状态都由独立的寄存器来表示，并且在任意时刻只有其中一位有效。
独热编码的优点：能够处理非数值属性；在一定程度上扩充了特征；编码后的属性是稀疏的，存在大量的零元分量。

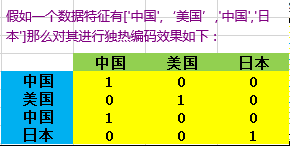
　　pandas的独热编码：
pandas.get_dummies(data, prefix=None, prefix_sep=’_’, dummy_na=False, columns=None, sparse=False, drop_first=False)
data : array-like, Series, or DataFrame
输入的数据
prefix : string, list of strings, or dict of strings, default None
get_dummies转换后，列名的前缀
columns : list-like, default None
指定需要实现类别转换的列名
dummy_na : bool, default False
增加一列表示空缺值，如果False就忽略空缺值
drop_first : bool, default False
获得k中的k-1个类别值，去除第一个
　　2.3.3标签编码

　　from sklearn.preprocessing LabelEncoder
LabelEncoder可以将标签分配一个0—n_classes-1之间的编码-不考虑数据间平等性

　　2.3.4多项式特征

　　from sklearn.preprocessing import PolynomialFeatures
简单理解多项式特征处理：就是一个数据集假如有a，b两个特征，那么对这个特征进行2次多项式特征处理的结果就是（1，ab,a2,b^2）PolynomialFeatures有三个参数:
degree：控制多项式的度,也就是多项式的最高次数，int类型
interaction_only： 默认为False，如果指定为True，那么就不会有特征自己和自己结合的项，上面的二次项中没有a2和b2。
include_bias：默认为True。如果为True的话，那么就会有上面的 1那一项。
　　2.3.5交叉验证

　　from sklearn.model_selection import cross_val_score


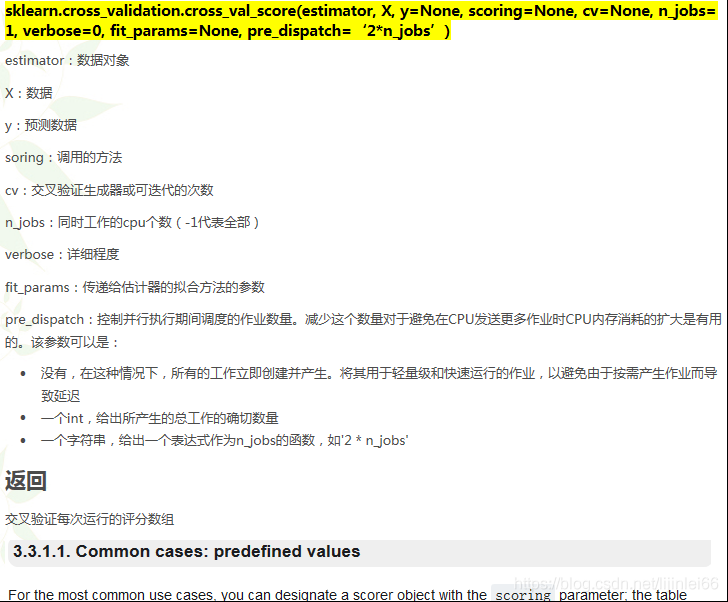
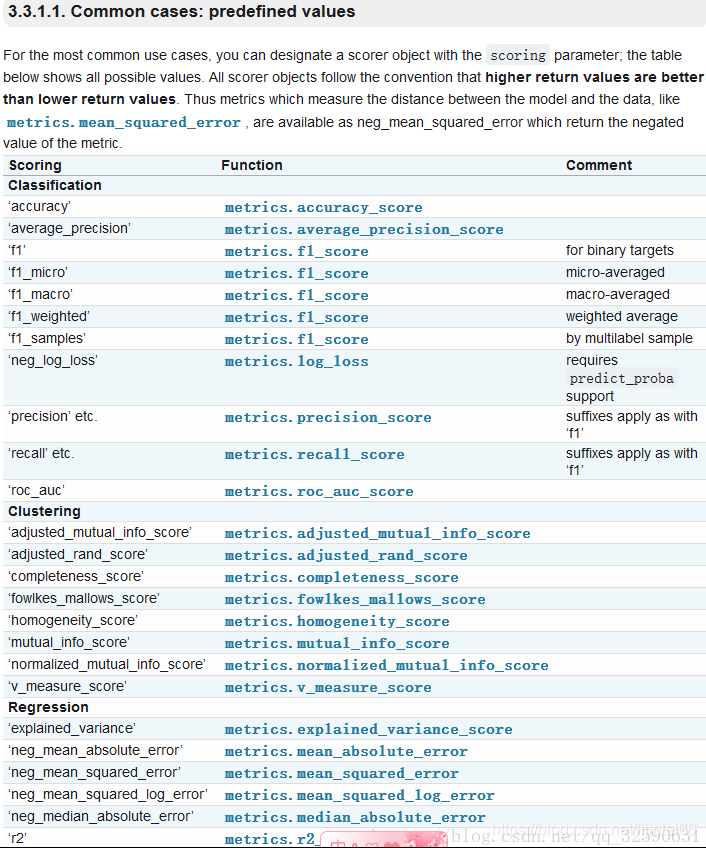
　　交叉验证种类：详细参考见此贴
train_test_split：在分类问题中，我们通常通过对训练集进行train_test_split，划分成train 和test 两部分，其中train用来训练模型，test用来评估模型，模型通过fit方法从train数据集中学习，然后调用score方法在test集上进行评估，打分；从分数上我们可以知道 模型当前的训练水平如何
—from sklearn.model_selection import train_test_split
X_train,X_test, y_train, y_test =train_test_split(train_data,train_target,test_size=0.4, random_state=0,stratify=y_train)
train_data：所要划分的样本特征集
train_target：所要划分的样本结果
test_size：样本占比，如果是整数的话就是样本的数量
random_state：是随机数的种子。
其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。比如你每次都填1，其他参数一样的情况下你得到的随机数组是一样的。但填0或不填，每次都会不一样。
随机数的产生取决于种子，随机数和种子之间的关系遵从以下两个规则：
种子不同，产生不同的随机数；种子相同，即使实例不同也产生相同的随机数。也可以对X，y进行切分
K-Fold Cross-validation k折交叉验证：简言之，就是进行多次train_test_split划分；每次划分时，在不同的数据集上进行训练、测试评估，从而得出一个评价结果；如果是5折交叉验证，意思就是在原始数据集上，进行5次划分，每次划分进行一次训练、评估，最后得到5次划分后的评估结果，一般在这几次评估结果上取平均得到最后的评分。k-fold cross-validation ，其中，k一般取5或10。
Stratified K-Fold Cross-validation 分层k折交叉验证：解决简单交叉验证带来的问题，所以进行分层交叉验证，保证每次划分中包含类别的比例数和原数据相同。如原数据有三类，比例为1：2：1，那么划分的k折中，每一折中的数据类别保持着1:2:1的比例，这样的验证结果更加可信。 实际上就是改变了交叉验证的划分函数。
Leave-one-out Cross-validation 留一法：留一法是一种特殊的交叉验证方式，顾名思义就是每次留下一个样本进行验证，如果样本容量是n 那么k折中的k等于n，进行n折交叉验证，适合小样本数据，耗时，相当于n折交叉验证，改变交叉验证数据划分函数即可。
　　2.3.6网格搜索

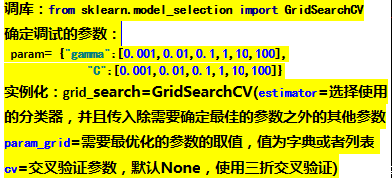
　　—from sklearn.model_selection import GridSearchCV
Grid Search：一种调参手段；穷举搜索：在所有候选的参数选择中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的结果。其原理就像是在数组里找最大值。（为什么叫网格搜索？以有两个参数的模型为例，参数a有3种可能，参数b有4种可能，把所有可能性列出来，可以表示成一个3*4的表格，其中每个cell就是一个网格，循环过程就像是在每个网格里遍历、搜索，所以叫grid search）

　　2.3.7管道机制

　　—from sklearn.pipeline import Pipeline

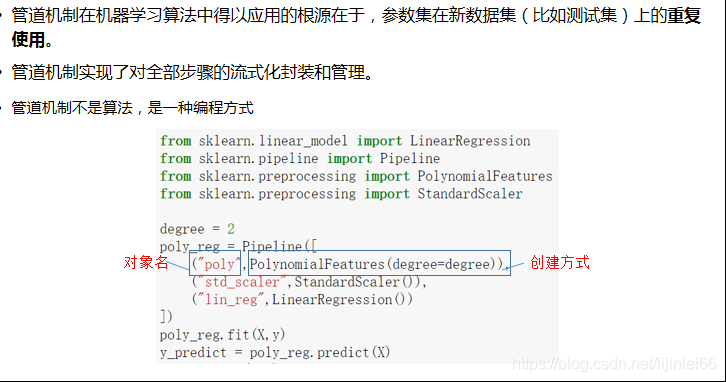
　　注意管道机制里面的参数写法是列表+元组的格式，列表用于存放所有的特征和算法处理的过程，元组具体写每个处理方式，每个管道机制中最多可以在最后添加一个算法，或者不填，格式如下：

　　2.4数据标准化、正则化


数据标准化　　数据标准化是将样本的属性缩放到某个指定的范围。
　　数据标准化的原因：
　　某些算法要求样本具有零均值和单位方差；
　　需要消除样本不同属性具有不同量级时的影响：①数量级的差异将导致量级较大的属性占据主导地位；②数量级的差异将导致迭代收敛速度减慢；③依赖于样本距离的算法对于数据的数量级非常敏感。
　　min-max标准化（归一化）：对于每个属性，设minA和maxA分别为属性A的最小值和最大值，将A的一个原始值x通过min-max标准化映射成在区间[0,1]中的值x’，其公式为：新数据=（原数据 - 最小值）/（最大值 - 最小值） from sklearn.preprocessing import MinMaxScaler
　　z-score标准化（规范化）：基于原始数据的均值（mean）和标准差（standarddeviation）进行数据的标准化。将A的原始值x使用z-score标准化到x’。z-score标准化方法适用于属性A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。新数据=（原数据- 均值）/ 标准差 from sklearn.preprocessing import StandardScaler
正则化——过拟合解决方案
数据正则化是将样本的某个范数（如L1范数）缩放到到位1，正则化的过程是针对单个样本的，对于每个样本将样本缩放到单位范数。
正则化包括L0、L1，L2正则：
L0正则化的值是模型参数中非零参数的个数。
L1正则化表示各个参数绝对值之和，可以将一些参数直接缩减为0
L2正则化标识各个参数的平方的和的开方值，可以将一些参数变得很小但是不为0
参数稀疏一个好处是可以简化模型，避免过拟合。因为一个模型中真正重要的参数可能并不多，如果考虑所有的参数起作用，那么可以对训练数据可以预测的很好，但是对测试数据就只能呵呵了。另一个好处是参数变少可以使整个模型获得更好的可解释性。为什么参数越小，说明模型越简单呢，这是因为越复杂的模型，越是会尝试对所有的样本进行拟合，甚至包括一些异常样本点，这就容易造成在较小的区间里预测值产生较大的波动，这种较大的波动也反映了在这个区间里的导数很大，而只有较大的参数值才能产生较大的导数。因此复杂的模型，其参数值会比较大。
稀疏的参数可以防止过拟合，因此用L0范数（非零参数的个数）来做正则化项是可以防止过拟合的。
从直观上看，利用非零参数的个数，可以很好的来选择特征，实现特征稀疏的效果，具体操作时选择参数非零的特征即可。但因为L0正则化很难求解，是个NP难问题，因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似，比L0容易求解，并且也可以实现稀疏的效果。

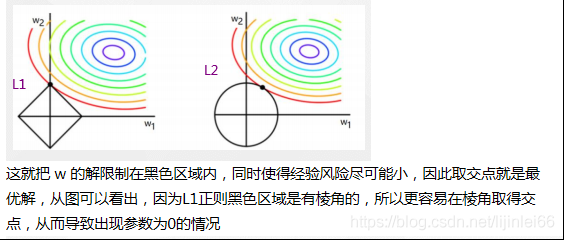
L1正则化-lasso(套索)回归

L2正则—Ridge（岭回归）
　　2.5 特征选择（降维）


　　从给定的特征集合中选出相关特征子集的过程称为特征选择。
　　进行特征选择的两个主要原因是：
　　减轻维数灾难问题；
　　降低学习任务的难度。
进行特征选择必须确保不丢失重要特征。
常见的特征选择类型分为三类：过滤式（filter）、包裹式（wrapper）、嵌入式（embedding）。
过滤式选择：该方法先对数据集进行特征选择，然后再训练学习器。特征选择过程与后续学习器无关。Relief是一种著名的过滤式特征选择方法。
包裹式选择：该方法直接把最终将要使用的学习器的性能作为特征子集的评价原则。其优点是直接针对特定学习器进行优化，因此通常包裹式特征选择比过滤式特征选择更好，缺点是由于特征选择过程需要多次训练学习器，故计算开销要比过滤式特征选择要大得多。
嵌入式选择
常见的降维方法：SVD、PCA、LDA