Error Detection and Correction
- Error Detection and Correction's Defination
- Error Detection 错误检测
- Block coding
- Hamming Distance
- Parity-Code
- Cyclic codes-CRC(Cyclic Redundancy Check)
- Checksum
- ERROR CORRECTION 错误纠正
- FORWARD ERROR CORRECTION
- Chunk Interleaving
Error Detection and Correction’s Defination 在通信阶段,Tx与Rx收发的信号不一致,则表明出现了错误(Error)
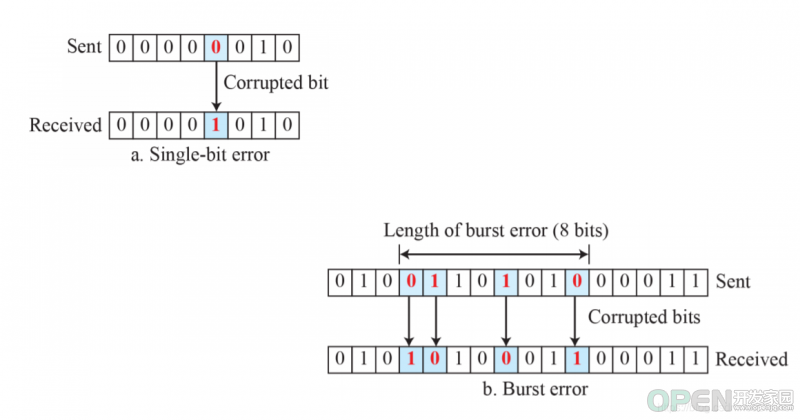
错误的种类可以分为两种,一种是只有一位bit发生反转(Signle-bit error);另一种是一个数据块中的复数个比特位反转(Burst error)。现实中,Single-bit error的出现频率远远小于Burst error。
Error Detection 错误检测
冗余(Redundancy):附加在通信数据后的一部分额外数据。用于差错校验。具体解释:当通信传输某数据时,如果对这个数据没有明确的定义(不知道数据位具体是0还是1),则使用冗余。Redundancy相当于事先定好的正确答案,而传输数据本身相当于问题,问题与答案一起传输过来,由于答案是已知的(对应的比特位是0还是1,传输错误也会立刻发现),所以可以将问题在Rx进行重新计算,得到的答案如果与正确答案不一致,则一定是问题出错了,也就说传输数据发生了error。
纠错过程比检错过程更复杂。因为检错只需要确认这个数据包是否有错误,而纠错需要知道错误的具体数目和所在位置。
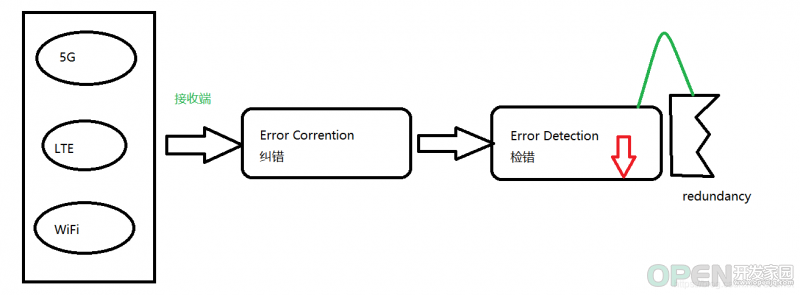
实际的通信过程中,Rx接收到来自于非有线网的数据后,会无条件进行一次纠错处理,经过该次处理后传输数据本身还有错误的概率就会大大降低,然后在配合冗余一起进行错误检测,与冗余结果不一致即有错误。由此可见冗余的重要性。
冗余的实现方法
通过各种编码方案来完成。宏观上可以分为Block Coding和Convolution Coding(回旋码)。快编码是将比特流分成块,多少bit相连视作一个单位,周期性的将比特流截断就可以生成多个数据块,冗余追加时则会在块的尾部追加,冗余的值取决于当前数据。而回旋码是将前面已经传输过去的数据为基础生成当前数据的冗余,冗余的值取决于之前发送的数据。Block coding比想象中性能要好,综合表现上还是Convolution性能更佳,但是复杂度也更高。
现在Block coding常用语检错而Convolution常用于纠错。当然他们本身的功能也支持用于常用之外的领域。
Block coding
- 格式:块数据被称为datawords,而冗余被称为redundant bits,二者结合被称为codewords。codewords就是块编码的基本单位。我们假设冗余位有r bits,而数据位有kbits令 r+k=n;则n一定大于k,因为有冗余且冗余不会为0。且块编码是one-to-one coding process,也就是说同一个dataword一定会得到一个相同的codewords,因为冗余是根据当前数据块生成的。而对于convolution coding由于冗余根据之前的数据来构成,就不满足相同的dataword生成固定的codeword这一现象。

- invalid coding:无效编码。2n-2k就是n位总数据-k位有效数据的差值。这个差值是无效数据,如果Rx接收到了无效数据,这说明有效数据一定在传输过程中破损。关于这个的理解,我们来看一下例题。

首先一个问题2n-2k是否等于2r?上图是8-4=4=22≠21,也就说与冗余位r无关。只是无效数据而已。
第二个问题,如何判断“就收到的数据是否有效”,来看例题:
dataword用1的个数来增加冗余位,如果1的个数是偶数则冗余位是0否则是1;得到了如表格所示的数据

然后分为以下几种情况:
- Rx接收到了011,是01的有效codewords
- Rx收到了011,但是由于错误导致其中1位bit反转,变成了111;此时由于111是无效数据(没有对应的有效数据就是无效数据),因此鉴定出有错误
- Rx收到了011,但是由于错位导致其中两位反转,变成了000,且000是有效数据,Rx错误识别了该数据,错误检测失败。
Hamming Distance

对两组数据进行异或运算后,其结果的1的个数就是Hamming distance的值。如果将其应用于错误检测环节,则可以使用它的变种Minimum Hamming Distance。
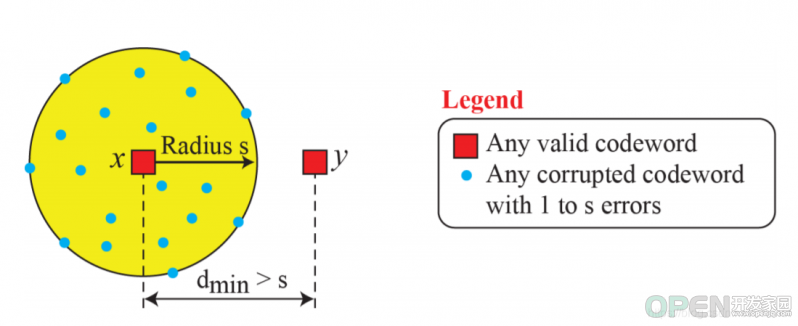
如果我们要保证能够检测到一组数据中的错误,则们我要求其Hamming distance的值最少是s+1,s是错误的位数。
举个例子来理解:

还是刚才的例题,这次我们引入一个新的概念——Linear Block Codes。即一个有效的codewords与另一个有效的codewords进行异或运算,得到的结果仍然是有效的codewords。我们可以拿任意两个有效数据进行XOR运算得到HD=2;又因为S=1所以1000%(仓帕森特)可以检测出1位bit发生错误的情况,这也正验证了我们刚才的假设,当错误2位以上时,Rx可能会误读数据而无法检测出错误。
Parity-Code
Parity-Code:奇偶校验码。当Linear Block Codes为偶数时k位dataword变为k+1为codeword时使用。可以检验出所有奇数个错误时出现的情况
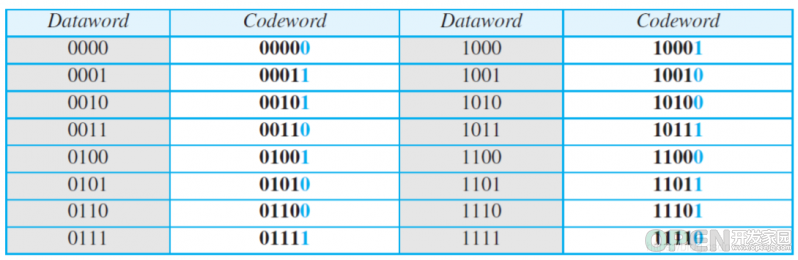
首先上图中HDmin=2,是偶数且满足dataword(k)与codeword(k+1)。规则是保证codewords的1的个数为奇数或者偶数,这里是偶数。然后当Rx接收到结果后,如果codewords的1的个数为奇数则一定是出错了。

新定义:校验子:Syndrome,codewords中0的个数是奇数则为1,为偶数则为0。

例题:发送1011,接收应该为10111
- 1011->10111 正常
- 1011->10011 有效数据1位错误,检测出错
- 1011->10110 冗余1位错误,检测出错
- 1011->00110 有效数据2位错误,未检测出错
- 1011->01011 有效数据3位错误,检测出错
Cyclic codes-CRC(Cyclic Redundancy Check)
循环码,举个例子1010是一个codewords,它的左移也是一个codewords。可以通过循环左移来生成不同的codewords,0101,1010,0101…
以此基础上CRC(Cyclic Redundancy Check)系统是当下阶段也在应用的错误检测方法,性能优良且目前暂无发展趋势,换言之当前的探测力度非常强。
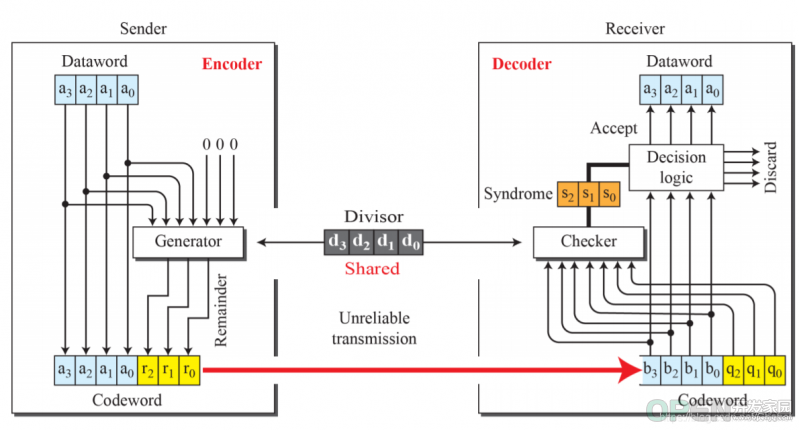
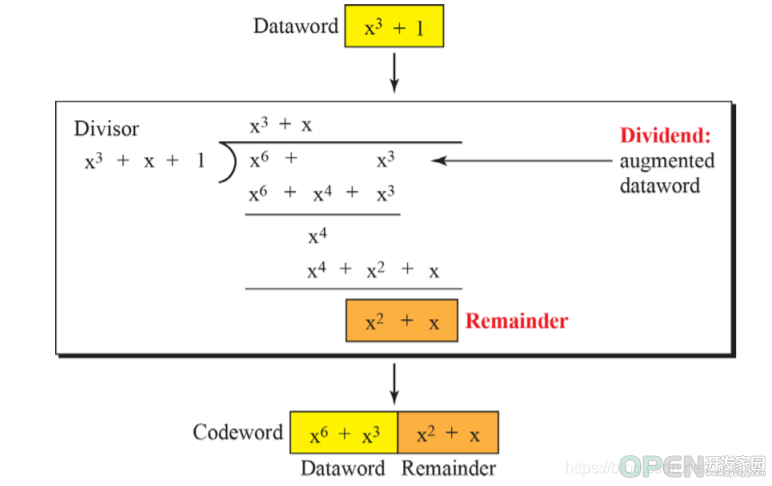
Tx的冗余位数并不是随机的,加入dataword有k位,codewords有n位,那么被除数的位数应该是n-k+1位。而冗余位数是n-k。
起初,Tx添加n-k位冗余位且全为0,然后添加到dataword后面进行二进制除法,除法规则与十进制相似,只不过商后运算的是异或而不是减法。
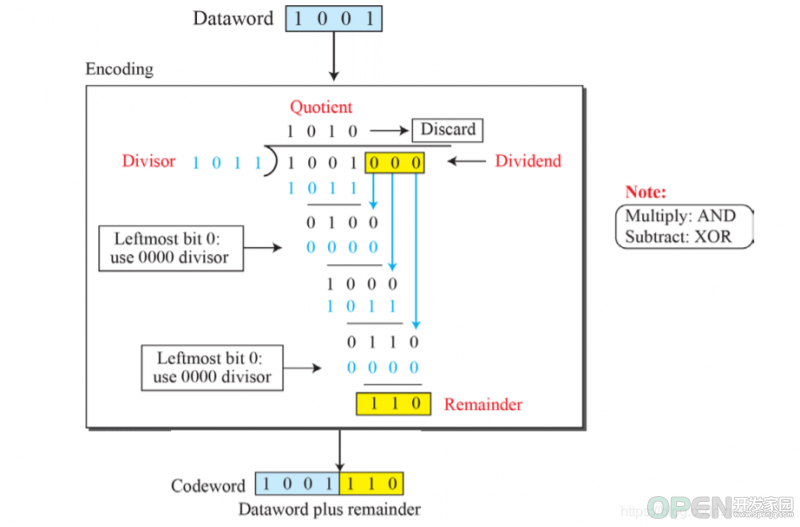
然后得到的n-k位数被称为Remainder(余数),这部分与要传输的数据结合在一起发送给接收端。接收端把收到的数据除以同一个相同的除数,余数为0这说明没有错误,否则就说明有错误。
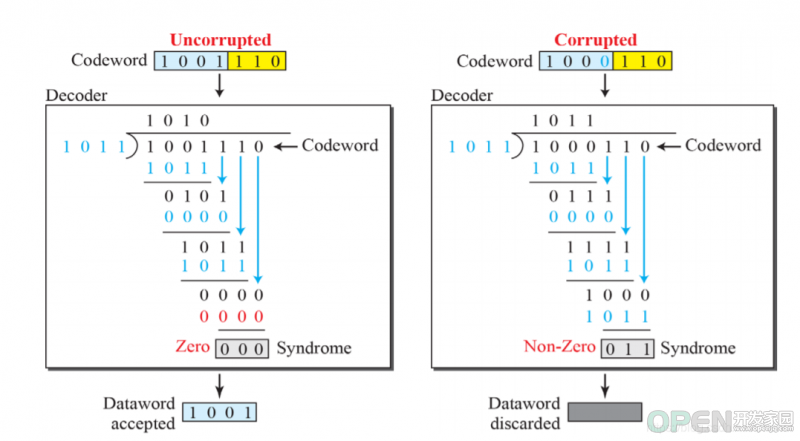
但是有时候n,k的值并不好确认,此时就需要探究CRC的数学原理了。
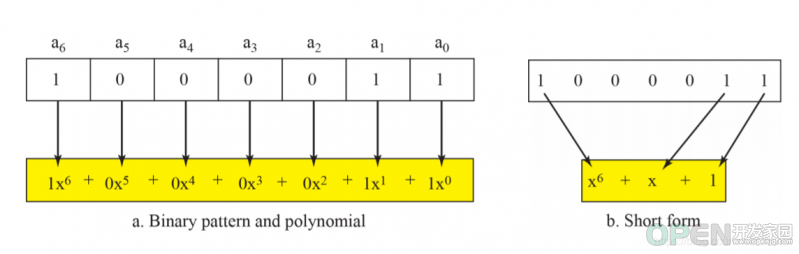
从右往左,是2的幂数递增。我们只保留非零项,可以将二进制数据转换为多项式的和。
虽然用多项式的和表示了出来,但是在计算过程中,加减法是XOR运算(同类型奇数个数为1,偶数个数为0【x4+x4=0】)而乘法则同标量乘法,除法同上面的CRC运算过程。例题如下。
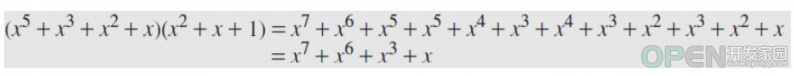
总结:

CRC无法抓到的错误:当错误多项式可以整除被除数或有x1以上的余数时,错误会被漏检。
运算过程中:
d x + s x = c x d_x+s_x=c_x dx+sx=cx
g x 的 位 数 = 该 多 项 式 的 最 高 次 数 g_x的位数=该多项式的最高次数 gx的位数=该多项式的最高次数
s x 的 位 数 = g x − 1 , 当 有 效 位 数 不 足 时 需 要 补 0 s_x的位数=g_x-1,当有效位数不足时需要补0 sx的位数=gx−1,当有效位数不足时需要补0
e x / g x = 0 , 则 无 错 误 e_x/g_x=0,则无错误 ex/gx=0,则无错误
包含因子x + 1的被除数可以检测所有奇数个数错误。[x4 + x2 + x + 1可以捕获所有奇数错误,因为它可以写成两个多项式x + 1和x3 + x2 + 1的乘积]
因此一个好的被除数,多项式生成器应该满足如下条件
1.它至少应该有两项
2. x0的系数应该是1
3.它不能除以在2和n - 1之间的xt + 1
4. 它应该有因式x + 1

Cyclic code在单个错误,两个错误,奇数个错误以及 burst errors[数据块中的错误] 中都有非常好的性能。它们可以很容易地在硬件和软件上实现,在硬件中实现尤其快,这使得循环码适合许多网络
Checksum
CRC的性能比Checksum要好,checksum是落后于CRC的错误探测技术。CRC主要应用在数据链路层(12阶层)而checksum主要应用于网络层(34阶层)。原因是由于网络是世界性的,改变网络的结构需要全世界的协调(不管发达国家还是网络发展非常差的国家),因此改变网络环境是困难的,但是数据链路层是本地的,改善本地网络是简单的,因此会出现这种情况。因特网的趋势,特别是在设计新协议方面,是用CRC来代替校验和。
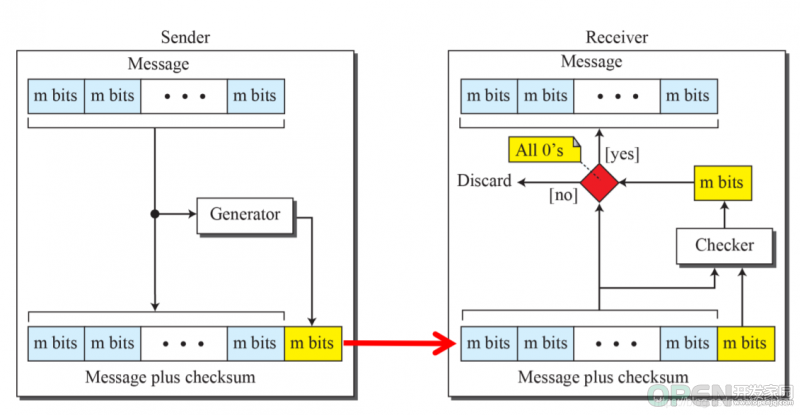
对于这项技术,简单而言,我们要传输的比特流以块为单位分割,每块等大。每块数据是m bits,我们把本次传输的这些个数据块求和得到一个数值,然后在这些数据块后追加一个等大的数据块,这个数据块是前面那些有效数据块的二进制数字矢量和的相反数。也就说所有mbit的数据块求和的数据的绝对值等于我们要添加的这个数据块的绝对值,他们之间互为相反数。这样当Rx收到数据块后,将最后一位数据与前面所有数据的和的值进行求和,得到值为0则认为传输阶段没有错误,否则认为传输出错。
来看一个例题

要传输的数据块的大小为4,(容量4bit)也就说每个数据块所能表示的数值最大为15. 然后我们现在计算给定的数据块之和(7.11.12.0.6)和为36。数值和为36,那么我们就要在后面追加一个数据块为-36,但是36这个值明显大于4bit,我们需要用等大的数据块大小来表现这个数值。此时使用的方法是shift:
36 = ( 32 + 4 ) 10 = ( 100100 ) 2 = 10 + 0100 36=(32+4)_{10}=(10 0100)_2=10+0100 36=(32+4)10=(100100)2=10+0100;这里利用shift左移,得到的结果是0110,而0110是数值6,我们为什么用数字6表示数字36呢?
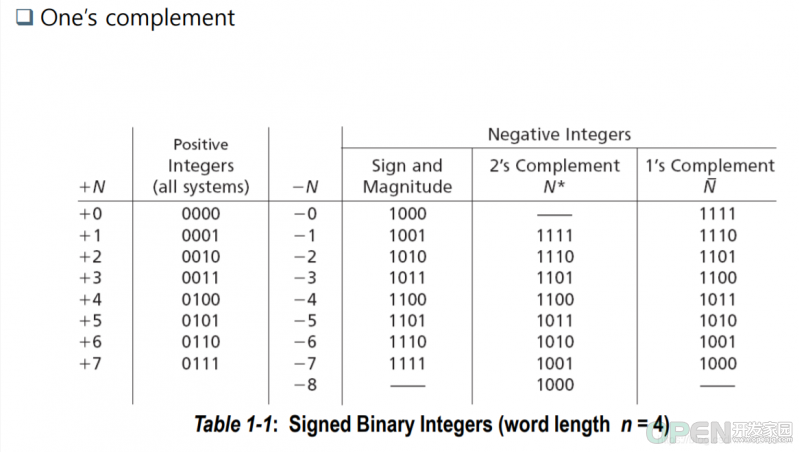
这里使用到了负数的表达方法:One’s Complement 即反码表示这个数字的负数,也就说这里的0110是负数6,那么它的反码就是1001(+9)
为什么会有这样的规定呢?我们来简化一下概念:
我们用A表示所有4-bits的数据块之和,Q表示A/24的商,R表示余数。则总结有式:
A = 2 4 × Q + R A=2^4 \times Q + R A=24×Q+R
C h e c k s u m = ( 2 4 − 1 ) − ( Q + R ) Checksum=(2^4-1)-(Q+R) Checksum=(24−1)−(Q+R)
24-1表达的是4bits数据能表达的最大数据1111也是负数0,因此对于接收端有:
A + C h e c k s u m = 2 4 × Q + R − ( 2 4 − 1 ) − ( Q + R ) A+Checksum=2^4 \times Q + R-(2^4-1)-(Q+R) A+Checksum=24×Q+R−(24−1)−(Q+R)
= 2 4 × Q 【 S h i f t 】 − ( 2 4 − 1 ) − Q = Q + ( 2 4 − 1 ) − Q =2^4 \times Q 【Shift】-(2^4-1)-Q=Q+(2^4-1)-Q =24×Q【Shift】−(24−1)−Q=Q+(24−1)−Q
= ( 2 4 − 1 ) = 1111 = − 0 =(2^4-1)=1111=-0 =(24−1)=1111=−0
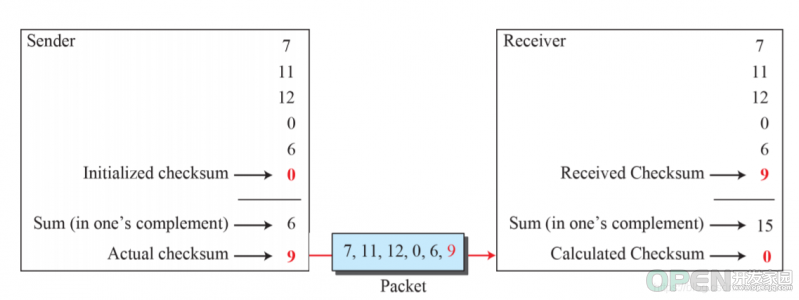
统合的角度上而言,我们得到的checksum为6,在one’s complement下为-6,表示位1001(实际上传输的值是9),接收端收到后36(0110)要加他的负值-6(1001),得到的结果是1111(-0),结果为0即传输无差错。
传统的校验和使用少量的位(16)来检测任何大小的消息中的错误(有时是数千位)。
缺点:如果一个word的值递增而另一个word的值递减相同的量,则无法检测到这两个错误,因为和和校验和保持不变.
ERROR CORRECTION 错误纠正
FORWARD ERROR CORRECTION
立即纠正错误或复制数据包
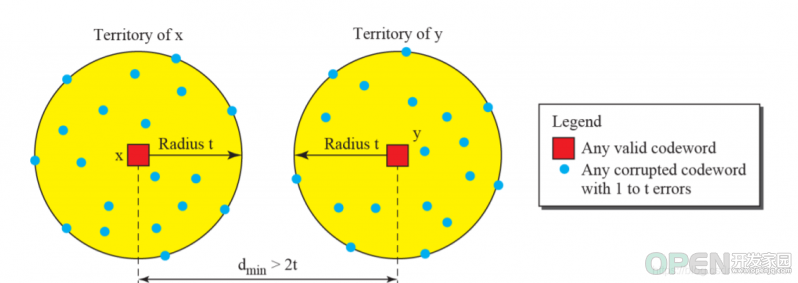
向前纠错或者正向纠错。纠错比检错更复杂,用之前的hamming distance解释,我们想要探知距离为s的错误则我们需要s+1的HD;而如果我们 想要纠正距离为t以内的错误,则需要2t+1的HD

这里做一下简单叙述,异或运算的结果往往都存在逆运算得到原数值的特点,这里的P表示的是带有CRC功能的数据包,也就说他们能够检测出是否传输中出现问题,当只有一个数据包在传输过程中出现问题时,可以用在Tx准备好的XOR运算结果R代替有错误的数据位进行异或运算,就可以逆算到出错的数据包Pi
当发送4个数据包时,我们只需要多发1个数据包(效率降低25%)但是却可以保证在1位出错是纠正错误,这样在这整体上而言效率还是非常好的。
Chunk Interleaving
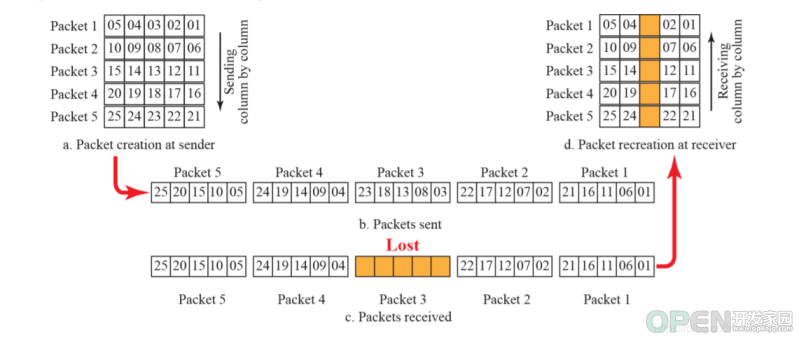
块交错:发送数据时,按位截断数据并组成新的数据包(行变成列),这样Rx收到后如果有数据包缺失,则根据对应的位补正即可(这样的优点在于纠错效率高),因为错误探测如果根据每个数据包进行探测具体某一位在效率上有影响。
纠错部分只做了简单描述,实际上现在使用的很多纠错方法都很复杂,理解起来比较难,在这就不作说明了。
| 
![]() 网络安全
发布于:2021-07-13 17:16
|
阅读数:441
|
评论:0
网络安全
发布于:2021-07-13 17:16
|
阅读数:441
|
评论:0

















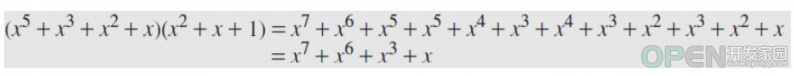










 QQ好友和群
QQ好友和群 QQ空间
QQ空间