研究大纲
- 介绍数据集和研究的目标
- 探索数据集
- 可视化
- 使用Chi-Square独立检验、Cramer's V检验和GoodmanKruskal tau值对数据集进行探索
- 预测模型,Logisitic回归和RandomForest
- 两个逻辑回归的实例
- 使用5折交叉验证对模型实例进行评估
- 变量选择改进
- 随机森林模型
- 用RandomForest和Logisitc回归进行预测
- 使用可视化进行最终的模型探索
- 结论和下一步措施
1.简介本报告是对心脏研究的机器学习/数据科学调查分析。更具体地说,我们的目标是在心脏研究的数据集上建立一些预测模型,并建立探索性和建模方法。但什么是心脏研究?
我们阅读了关于FHS的资料:
心脏研究是对社区自由生活的人群中心血管疾病病因的长期前瞻性研究。心脏研究是流行病学的一个里程碑式的研究,因为它是第一个关于心血管疾病的前瞻性研究,并确定了风险因素的概念。
该数据集是FHS数据集的一个相当小的子集,有4240个观测值和16个变量。这些变量如下:
- 观测值的性别。该变量在数据集中是一个名为 "男性 "的二值。
- 年龄:体检时的年龄,单位为岁。
- 教育 : 参与者教育程度的分类变量,有不同的级别。一些高中(1),高中/GED(2),一些大学/职业学校(3),大学(4)
- 目前吸烟者。
- 每天抽的烟的数量
- 检查时使用抗高血压药物的情况
- 流行性中风。流行性中风(0 = 无病)。
- 流行性高血压(prevalentHyp)。流行性高血压。如果接受治疗,受试者被定义为高血压
- 糖尿病。根据第一次检查的标准治疗的糖尿病患者
- 总胆固醇(mg/dL)
- 收缩压(mmHg)
- 舒张压(mmHg)
- BMI: 身体质量指数,体重(公斤)/身高(米)^2
- 心率(次/分钟)
- 葡萄糖。血糖水平(mg/dL)
最后是因变量:冠心病(CHD)的10年风险。
这4240条记录中有3658条是完整的病例,其余的有一些缺失值。
2.了解数据的意义在每一步之前,要加载所需的库。require(knitr)
require(dplyr)
require(ggplot2)
require(readr)
require(gridExtra) #呈现多幅图
然后,加载心脏研究的数据集。
2.1 变量和数据集结构的检查
我们对数据集进行一次检查。dim(dataset)
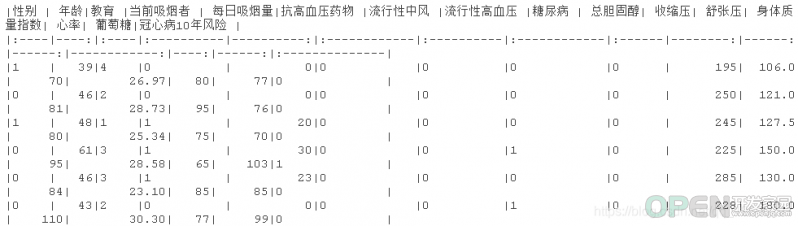
kable(head(dataset))
str(dataset)
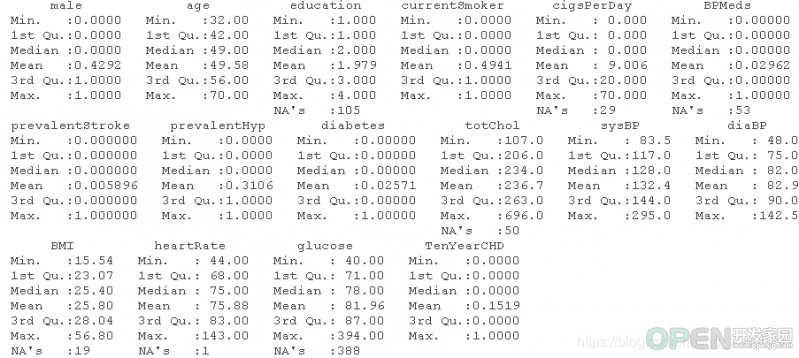
##检查变量的摘要
summary(dataset)
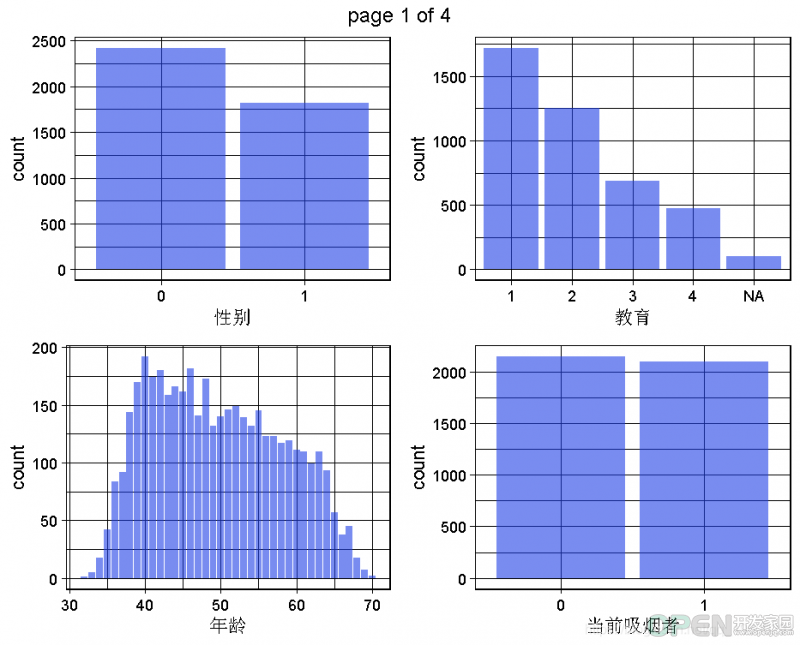
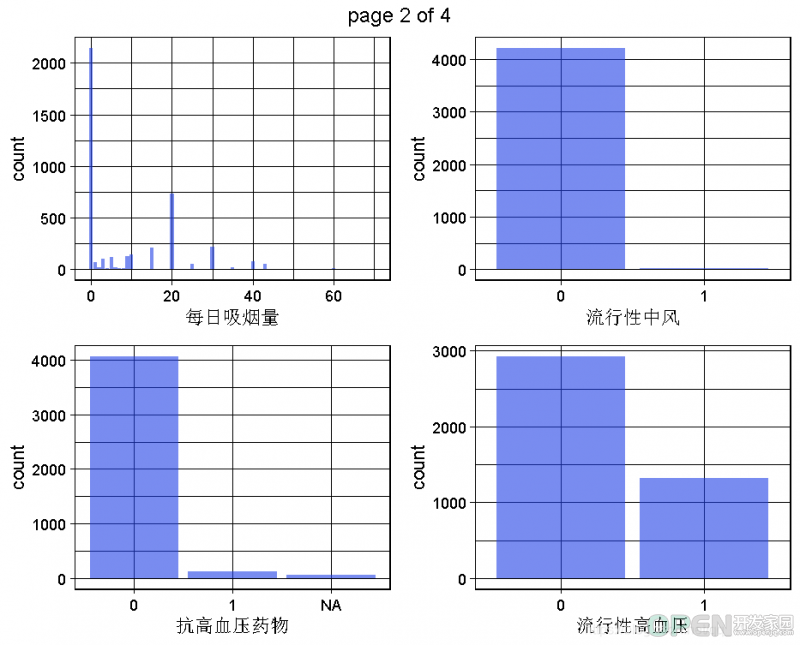
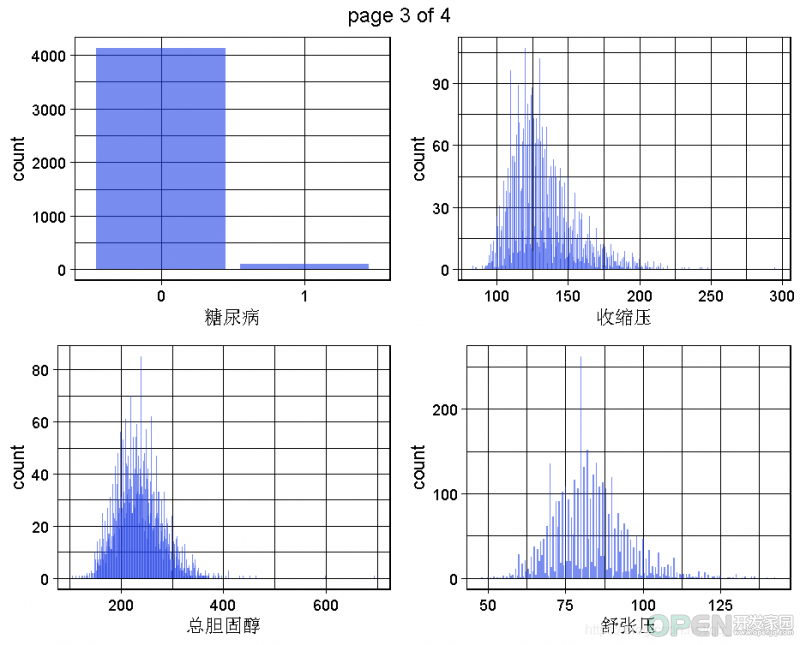
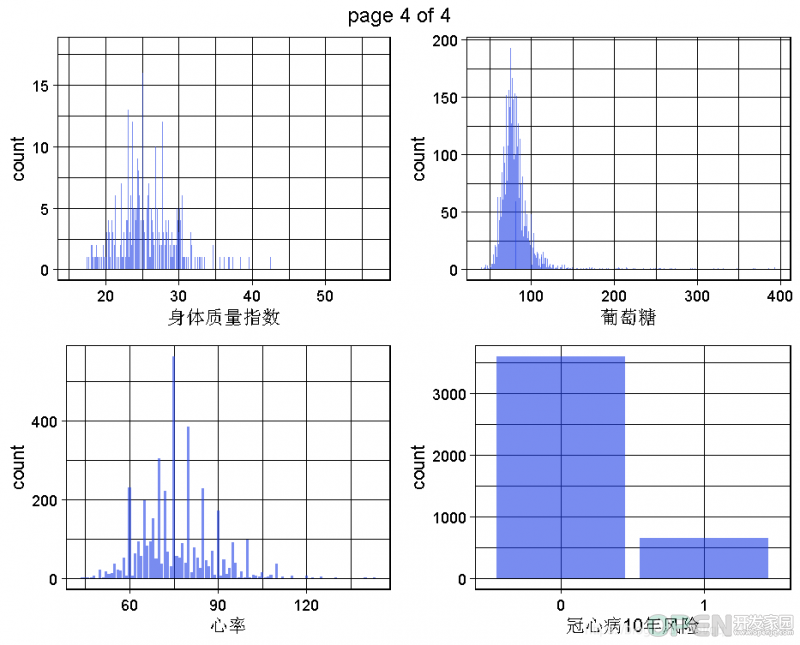
2.2 数据集的单变量图
生成一个数据集的所有单变量图。# 需要删除字符、时间和日期等变量
geom_bar(data = dataset,
theme_linedraw()+
#colnames(dataset)
marrangeGrob(grobs=all_plots, nrow=2, ncol=2)
这是为了获得对变量,对整个问题和数据集的理解,将通过多变量或至少双变量的可视化来实现。
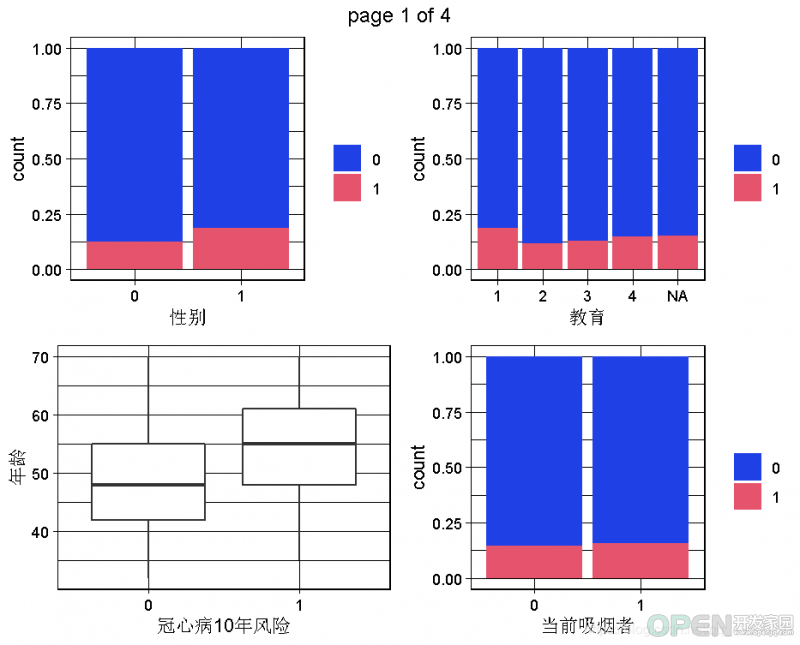
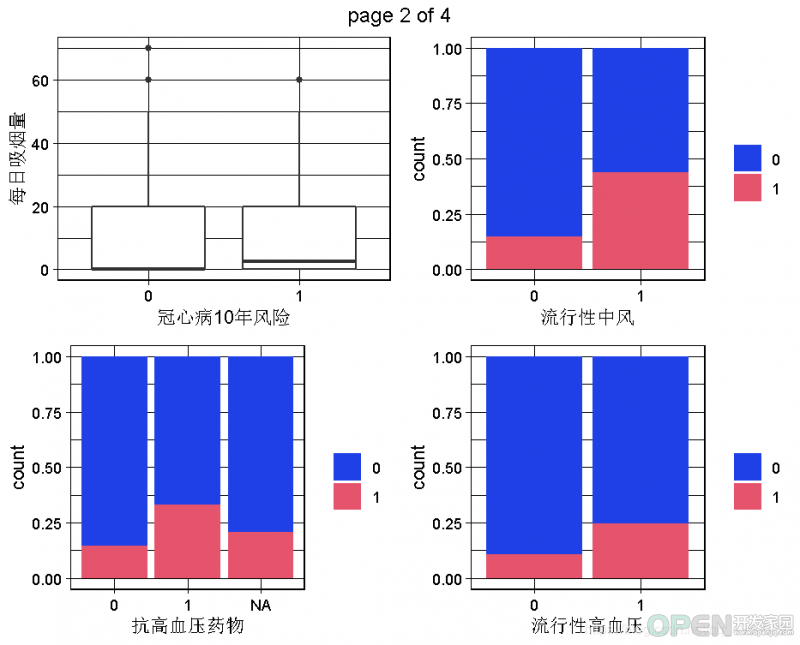
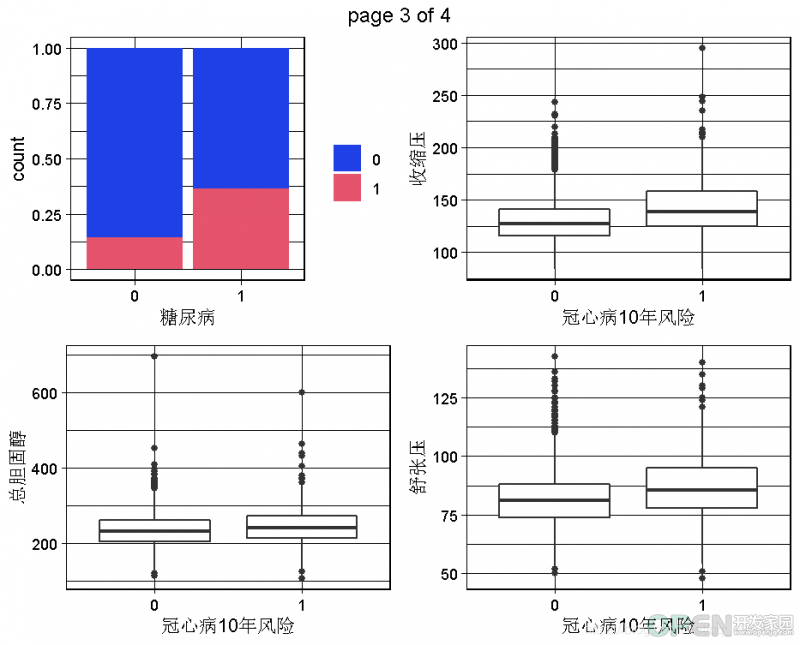
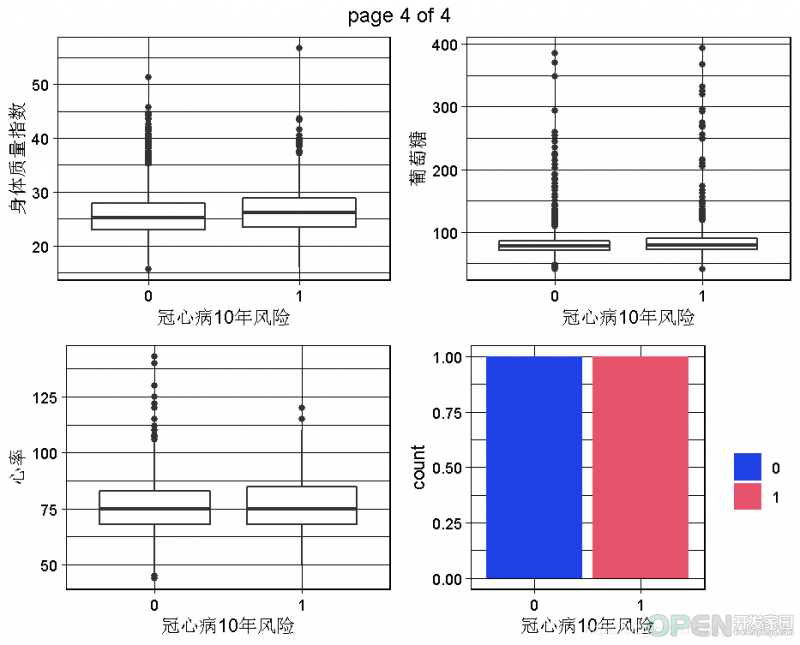
2.3 数据集的双变量图:因变量和预测因素之间的关系
现在我们可以进行一些双变量的可视化,特别是为了看到因变量(TenYearCHD)和预测因素之间的关系。由于图的数量太多,不是所有的一对变量都能被调查到!我们可以在后面的步骤中继续调查。我们可以稍后再回到这一步,深入了解。
下面的代码可以生成因变量的所有双变量图。由于因变量是一个二元变量,所以当预测变量是定量的时候,我们会有boxplots,或者当预测变量是定性的时候,我们会有分段的bar图。for (var in colnames(dataset) ){
if (class(dataset[,var]) %in% c("factor","logical") ) {
ggplot(data = dataset) +
geom_bar( aes_string(x = var,
} else if (class(dataset[,var]) %in% c("numeric","double","integer") ) {
ggplot(data = dataset) +
geom_boxplot()
根据我们掌握的情况,男性与TenYearCHD直接相关,因此男性这个变量似乎是一个相对较好的预测因素。同样,年龄似乎也是一个很好的预测因素,因为TenYearCHD == TRUE的病人有较高的年龄中位数,其分布几乎相似。相反,不同类别的教育和因变量之间似乎没有关系。目前的吸烟者变量与因变量有轻微的关系,因为目前的吸烟者患TenYearCHD的风险略高。
2.4 使用Goodman&Kruskal tau检验定性变量之间的关系
然而,除了这些本质上是定性方法的图表外,人们可能希望对这种关联有一个数字值。为了有这样的数字测量,我想使用Goodman&Kruskal的tau测量,这是两个无序因子,即两个分类/名义变量之间的关联测量。在我们这个数据集中的因子变量中,只有教育是序数变量,即它的类别有意义。这种测量方法比Cramer's V或chi-square测量方法更具信息量。GKtauData(cat_variables)
plot(dataset)
可以看出,关于因变量的变异性,预测因素的解释力非常小。换句话说,根据Goodman和Kruskal's tau度量,我们的预测因素和因变量之间几乎没有关联。这可以从TenYearCHD一栏的数值中看出。
假设我的G&Ktau检验正确的话,这对模型来说并不是一个好消息。
为了检验这些发现,我们可以用Chi-square检验来检验分类变量与因变量的关联的显著性,然后用Phi相关系数来评估可能的关联的强度。Phi用于2x2等值表。对于更大的表格,即有更多层次的变量,可以利用Cramer's V。chisq.test(table(dataset_cat$p.value ))
phi(matrix(table(dataset_cat_variables[,7],
奇怪的是,当Chi-square的P值如此之低时,可能的关联的显著性为零。这两个测试(Chi-square和Phi相关)在大量的观察中基本上得出相同的结果,因为一个是基于正态分布的,另一个是基于t分布的。
2.5 多重共线性的双变量分析
该模型的真正问题在于共线性现象。共线性关系发生在两个预测因子高度相关的情况下。我们需要检查这种特性,然后继续建立对数回归模型。
根据Goodman和Kruskal's tau图,我们不应该担心共线性。但是,有序变量的教育变量呢?Cramer's V检验显示,其强度不大。# 教育与其他分类变量的Chi square独立性测试
chisq.test(table(education,variables[,x]))$p.value )
#将教育变量重新定位到数据集的第一个变量上
assocstats(x = table(dataset_cat_variables[,1], dataset_$cramer ) )
没有一个变量显示与教育有很强的关联。Cramer's V的最高值是0.145,这在教育和性别之间是相当弱的。
但是诸如currentSmoker和cigsPerDay这样的变量呢?很明显,其中一个是可以预测的。有一个数字变量和一个分类变量,我们可以把数字变量分成几个类别,然后使用Goodman和Kruskal's tau。GroupNumeric()函数可以帮助将定量变量转换成定性变量,然而,基于对数据的主观理解,以及之前看到的cigsPerDay的多模态分布,在这里使用cut()函数很容易。
现在让我们检查一下GKtau的数值class_list <- lapply(X = 1:ncol(dataset_2), function(x) class(dataset_2[,x]))
t <- sapply(X = names(class_list) , FUN = function(x) TRUE %in% ( class_list[x] %in% c("factor","logical")) )
dataset_cat_variables_2 <- subset(x = dataset_2, select = t )
plot(dataset_2)
从矩阵图上的tau值及其背景形状,我们可以看到cigsPerDay可以完全解释currentSmoker的变异性。这并不奇怪,因为如果我们知道一个人每天抽多少支烟就可以断言我们知道一个人是否是吸烟者!
第二个关联是cigsPerDay与男性的关系,但它并不强烈。因此,前者可以解释后者的较小的变化性。
在下一个数据集中,我把所有定量变量转换成定性/分类变量。现在我们可以有一个全面的矩阵,尽管由于转换,一些信息会丢失。dataset_3$totChol <- GroupNumeric(x = dataset$totChol , n = 5 )
我们可以看到,sysBP和diaBP可以预测prevalentHyp,但不是很强。(0.5左右)。因此我们可以在模型中保留prevalentHyp。第二点是关于GK tau的输出。
3.预测模型:Logistic回归和RandomForest现在是评估模型实例的时候了。在这里,我们把逻辑回归称为模型。
我们有两个实例。
1. 一个包括所有原始变量的模型实例,特别是cigsPerday和currentSmoker变量
2. 一个包括所有原始变量的模型实例,除了currentSmoker,cigsPerday被转换为一个因子变量
为了评估模型实例,我们可以使用数学调整训练误差率的方法,如AIC。另一种方法是使用验证数据集,根据模型在这个数据集上的表现来评估模型。在后一种方法中,我选择使用K-fold Cross-Validation(CV)技术,更具体地说是5-fold CV。在这里,还有其他一些技术,如留一法交叉验证。
3.1 两个Logistic回归模型实例# 因为下一步的cv.glm()不能处理缺失值。
# 我只保留模型中的完整案例。
dataset_1 <- dataset[complete.cases(dataset),]
glm(TenYearCHD ~ . , family = "binomial")
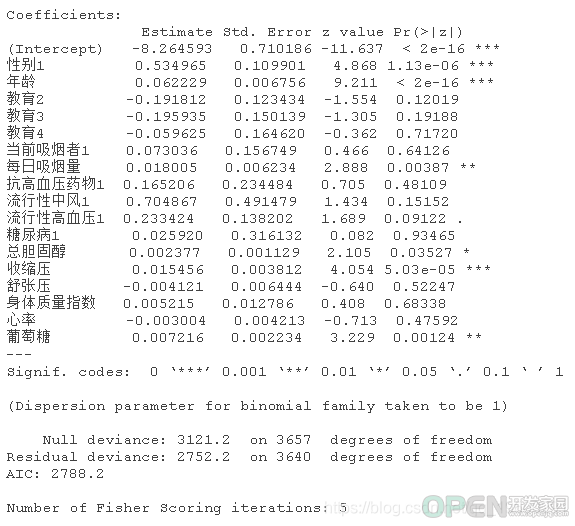
这个模型是基于原始数据集的。有缺失值的记录被从数据集中省略,模型显示变量男性、年龄、cigsPerDay、totChol、sysBP和葡萄糖是显著的,而prevalentHyp在某种程度上是显著的。glm(formula = TenYearCHD ~ . , family = "binomial")
在第二个模型实例中,重要变量与前一个模型实例相同。
一个非常重要的问题是,如何衡量这两个模型实例的性能以及如何比较它们?有各种方法来衡量性能,但我在这里选择了5折交叉验证法。
为了进行交叉验证和评估模型实例,我们需要一个成本函数。boot软件包推荐的一个函数,是一个简单的函数,它可以根据一个阈值返回错误分类的平均数。阈值默认设置为0.5,这意味着任何观察到的超过50%的CHD机会都被标记为有持续疾病的TRUE病例。从医学的角度来看,我把阈值降低到0.4,这样即使是有40%机会得心脏病的病例,也会被标记为接受进一步的医疗关注。降低阈值,增加了假阳性率,从而增加了医疗费用,但减少了假阴性率,挽救了生命。我们可以使用敏感度或特异性作为成本函数。此外,也可以使用cvAUC软件包将曲线下面积(AUC)与CV结合起来。
3.2 模型实例的交叉验证评估model1_cv_delta <- cv.glm( model1, cost = cost, K = 5)$delta[1]
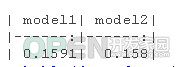
kable(data.frame("model1" = model1_cv_delta ,
kable(
caption = "CV-Accuracy", digits = 4)
我们可以看到,两个模型非常相似,然而,模型2显示出轻微的优势。准确率确实相当高。但是,让我们看看我们是否可以通过删除一些变量来改进model1。
3.3 通过变量选择改进模型
我们看一下model1的总结。summary(model1)
到现在为止,我们一直假设所有的变量都必须包含在模型中,除非是共线性的情况。现在,我们被允许通过删除不重要的变量。这里有几种方法,如前向选择和后向选择。
例如,后向选择法是基于不显著变量的P值。淘汰继续进行,直到AIC显示没有进一步改善。还有stats::step()和bestglm::bestglm()函数来自动进行变量选择过程。后者的软件包及其主要函数有许多选择信息标准的选项,如AIC、BIC、LOOCV和CV,而前者的逐步算法是基于AIC的。bestglm(Xy = dataset_1 , family = binomial , IC = "BIC")
step(object = model1 )
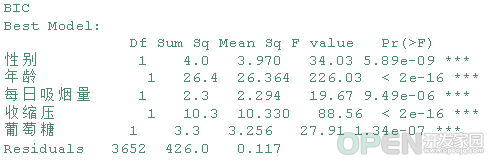
现在让我们来看看这两个模型和它们的交叉验证误差。bestglm_bic_model
基于BIC的bestglm::bestglm()将模型变量减少到5个:男性、年龄、cigsPerDay、sysBP和葡萄糖。所有的变量都是非常显著的,正如预期的那样。summary(step_aic_model)
基于AIC的step()函数将模型变量减少到8个:男性、年龄、cigsPerDay,prevalentStroke、prevalentHyp、totChol、sysBP和glucose。值得注意的是,通过step()找到的最佳模型实例具有不显著的变量。
glm_cv_error <- cv.glm(
glmfit = glm(formula
family = binomial, data = dataset_1),
step_cv_error <- cv.glm(glmfit = step_aic_model, cost = cost, K = 5)$delta[1]
kable(bestglm_model_cv_error ,
step_model_cv_error )
)
交叉验证误分类误差
kable(data.frame("bestglm() bic model"
"step() aic model"
交叉验证-准确度
AIC方法和BIC方法都能产生相同的准确性。该选择哪种方法呢?我宁愿选择AIC,因为该模型实例有更多的预测因素,因此更有洞察力。然而,选择BIC模型实例也是合理的,因为它更简明。与model1的准确度相比,我们通过变量选择在准确度上有0.8475-0.842=0.00550.8475-0.842=0.0055的提高。然而,我们失去了关于其他预测因子和因变量关系的信息。
3.4 RandomForest模型
到目前为止,我只做了逻辑回归模型。有更多的模型可以用来为当前的问题建模,而RandomForest是一个受欢迎的模型。让我们试一试,并将结果与之前的模型进行比较。#---- 差是每个RF模型实例的CV输出的错误分类率
#---- 每个选定的树的CV错误分类率的最终结果被绘制出来
# 对于不同数量的树,我们计算CV误差。
for (n in seq(50,1000,50))
for (k in 1:5)
rf_dataset_train <- dataset_1[fold_seq != k ,]
rf_dataset_test <- dataset_1[fold_seq == k , ]
rf_model <- randomForest( formula,
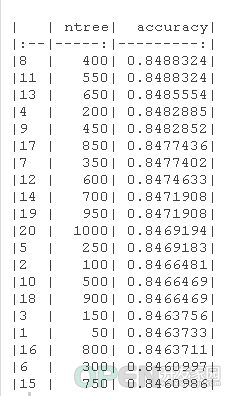
kable(rf_df[sort(x = rf_df[,2])
#----- 误差基于RandomForest OOB,即RandomForest输出的混淆矩阵
for (n in seq(50,1000,50)) {
counter <- counter + 1
rf_model <- randomForest( formula ntree = n, x =
}
ggplot() +
geom_point(data = rf_df , aes(x = ntree , y = accuracy)
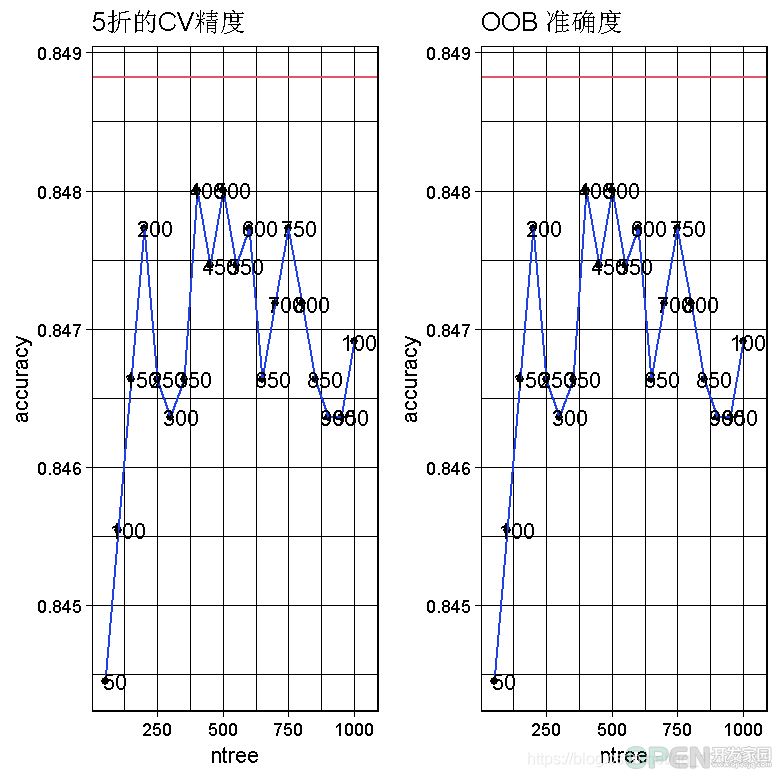
在这里,我同时使用了CV和out-of-bag(OOB)来评估随机森林性能。
我们可以看到,在50到1000棵树的范围内,RandomForest模型的最高精度可以通过设置CV方法的树数等于400来获得。图中的红线显示了我们从逻辑回归模型实例中得到的最佳CV精度。由于OOB的最高准确率高于CV的最高准确率,所以我选择了CV的准确率,使其更加谨慎。ntree=400的CVaccuracy=0.8486CVaccuracy=0.8486,比最好的逻辑回归模型差0.00020.0002! 然而,如果我们考虑OOB的准确性,那么RandomForest模型比最佳逻辑回归模型好0.00120.0012。
在RF中,模型的准确性有所提高,但代价是失去了可解释性。RF是一个黑箱,我们无法解释预测因子和因变量之间的关系。
3.5 模型对个人数据如何预测?
这里为了完成这个报告,我想在一个新的数据集上增加一个预测部分。该数据集只有一条记录,其中包括我自己的个人数据。换句话说,我已经创建了一个模型,我想知道它是否预测了我的CHD。> pred_data$年龄 <- 31
> pred_data$教育 <- factor(4, levels = c(1,2,3,4))
> pred_data$当前吸烟者 <- FALSE
> pred_data$每日吸烟量 <- 0
> pred_data$抗高血压药物 <- FALSE
> pred_data$流行性中风 <- FALSE
> pred_data$流行性高血压 <- FALSE
逻辑回归模型的预测输出。glm_BIC_opt <- glm(data = dataset_1 , formula ,family = binomial )
predict(glm_BIC_opt, newdata = pred_data)
随机森林预测。rf_model <- randomForest( formula = . ,
predict(rf_model, pred_data)
因此,现在看来,我没有风险! 然而,正如我之前提到的,这些模型是为了教育和机器学习的实践,而不是为了医学预测!所以,我认为这些模型是有价值的。
4.最终模型探索让我们最后看一下这个模型dataset_3 <- dataset_2[complete.cases(dataset_2),]
dataset_3_GK <-
plot(dataset_3_GK)
ggpplot(data = dataset , text.angle = 0,label.size =2 , order = 0 ) +
scale_colour_manual(values = color)+
scale_fill_manual(values = color)
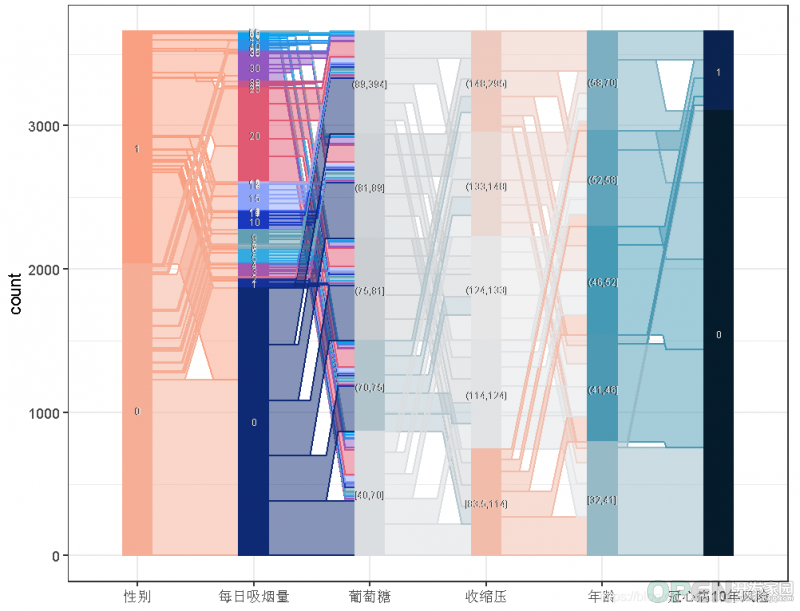
结果大多符合预期。根据GKtau值,预测因子之间的关联最小。这正是我们想要的,以避免共线性现象。
然而,平行坐标仍然显示了一些有趣的点。例如,年龄组与 "十年健康发展 "结果之间的关联很有意思。较低的年龄组在TenYearCHD==TRUE中的参与度很低,这意味着年龄与该疾病有正相关。另一方面,与男性相比,女性(男性==FALSE)在0支烟和[1,20]支烟组的贡献更大。换句话说,男性倾向于抽更多的烟,而且是重度吸烟者。
桑吉图可以产生更好的洞察力,因为我们可以沿着坐标轴观察样本。
5.结论在这项研究中,为了建立预测模型,使用了包括4240个观测值和16个变量的心脏研究的数据集。这些模型旨在预测十年后的冠心病(CHD)。
在对数据集进行探索后,利用逻辑回归和随机森林模型来建立模型。使用K-Fold Cross-Validation对模型进行了评估。
为了扩展这项研究,可以使用进一步的分类方法,如支持向量机(SVM)、梯度提升(GB)、神经网络模型、K-近邻算法,甚至决策树。
| 
![]() 编程语言
发布于:2021-07-13 23:42
|
阅读数:780
|
评论:0
编程语言
发布于:2021-07-13 23:42
|
阅读数:780
|
评论:0




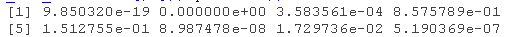












 QQ好友和群
QQ好友和群 QQ空间
QQ空间