朴素贝叶斯(Naive Bayesian Mode,NBM) 贝叶斯由来 朴素贝叶斯 贝叶斯定理 与特征条件独立 假设的分类方法。优点是在数据较少的情况下仍然有效,可以处理多类别的问题。缺点是对于输入数据的装备方式较为敏感。适用于标称型的数据。贝叶斯定理
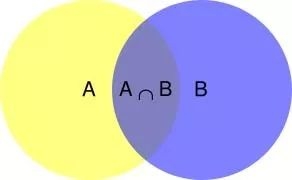
P(A) 是 A 的先验概率或边缘概率,不考虑 B 的因素 P(A|B) 是已知 B 发生后 A 的条件概率,也称作 A 的后验概率。 P(B|A) 是已知 A 发生后 B 的条件概率,也称作 B 的后验概率,称作似然度。 P(B) 是 B 的先验概率或边缘概率,称作标准化常量。 P(B|A)/P(B) 称作标准似然度。 示例1:桶中的石子
示例2:根据天气情况判断是否出去游玩
统计出去游玩的特征概率 计算游玩概率
统计不出去游玩的特征概率 P(否) 的概率。计算不游玩概率
概率比较 1/4 * 3/4 1/4 2/5) / (3/5 * 2/5 2/5 1/2) < (1/2 * 1/2 1/6 2/3 * 3/5) / (3/5 2/5 2/5 * 1/2) 所以 P(是|多云、冷、低、弱) < P(否|多云、冷、低、弱)。Python 实现 需要选择样本,如:示例2中的天气样本 计算每个类别的概率,这是先验概率 计算每个特征和类别同时发生的概率,这是后验概率 计算条件概率 比较特征出现在类别的概率 import pandas as pdimport numpy as npclass Nbm(object): def getSampleSet(self): dataSet = np.array(pd.read_csv('csv文件')) #将数据转为数组 featureData = dataSet[:, 0 : dataSet.shape[1] - 1] #取出特征 labels = dataSet[:, dataSet.shape[1] - 1] #取出类别 return featureData, labels def priori(self, labels): # 求出是和否的先验概率 labels = list(labels) priori_ny = {} for label in labels: priori_ny[label] = labels.count(label) / float(len(labels)) # P = count(label) / count(labels) return priori_ny def feature_probability(self, priori_ny, features): # 求出特征概率:多云+是,多云+否,冷+是,冷+否同时发生的概率 p_feature_ny = {} for ny in priori_ny.keys(): ny_index = [i for i, label in enumerate(labels) if label == ny] # 是、否的下标 for j in range(len(features)): f_index = [i for i, feature in enumerate(trainData[:, j]) if feature == features[j]] # 特征的下标 xy_count = len(set(f_index) & set(ny_index)) # 类别和特征下标相同的长度 pkey = str(features[j]) + '+' + str(ny) p_feature_ny[pkey] = xy_count / float(len(labels)) # 特征和类别同时发生的概率 return p_feature_ny def conditional_probability(self, priori_ny, feature_probability, features): #求出条件概率 P = {} for y in priori_ny.keys(): for x in features: pkey = str(x) + '|' + str(y) P[pkey] = feature_probability[str(x) + '+' + str(y)] / float(priori_ny[y]) # P[X1/Y] = P[X1Y]/P[Y] return P def classify(self, priori_ny, feature_probability, features): #求条件概率 p = self.conditional_probability(priori_ny, feature_probability, features) #求出[多云、冷、低、弱]所属类别 f = {} for ny in priori_ny: f[ny] = priori_ny[ny] for x in features: f[ny] = f[ny] * p[str(x)+'|'+str(ny)] #计算P(多云∣是)∗P(冷∣是)∗P(低∣是)∗P(弱∣是)∗P(是) return max(f, key=f.get) #概率最大值对应的类别if __name__ == '__main__': nbm = Nbm() features = ['多云', '冷', '低', '弱'] trainData, labels = nbm.getSampleSet() priori_ny = nbm.priori(labels) feature_probability = nbm.feature_probability(priori_ny, features) result = nbm.classify(priori_ny, feature_probability, features) print(features, '的结果是', result)总结 参考资料 代码地址 系列文章 
![]() 编程语言
发布于:2021-06-24 09:56
|
阅读数:558
|
评论:0
编程语言
发布于:2021-06-24 09:56
|
阅读数:558
|
评论:0



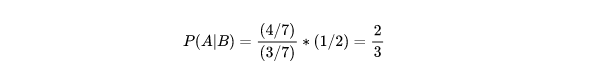



 QQ好友和群
QQ好友和群 QQ空间
QQ空间