初夏小谈：排序算法---基数排序（小白也能看懂）

小蚂蚁

在海量数据随机分布时进行排序时最快的当属桶排序因为它的时间复杂度是O(n)也就是只需两趟就可以将所有数据排好，今天所说的就是基于桶排序的思想进行基数排序。
基数排序：就是每次按照其各个位上的大小进行的一次排序，每一次排完后就将排完后的数据重新放回去，接着进行十位上的数字比较大小来在进行一次排序，然后再放回去。。。后面都是这样不断的排序一次，又接着放回去，直到把数组中最大数的位数排完。此时这一系列数字就已经排序完成。




我以12,63,156,982,20,478,639,32,2315,123 这十个数为例进行排序：

刚开始我找到最大的数2315并且记录它有多少位。这个位数就是一共循环往桶里放的次数

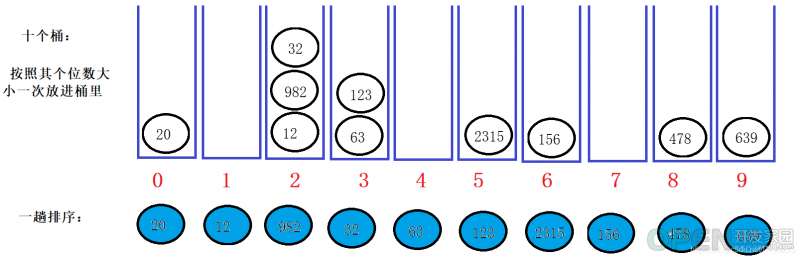
第一次排序我将所有数据按照其个位上的大小进行排序依次放进桶中，并且将排序完成后的重新放回原位置上。

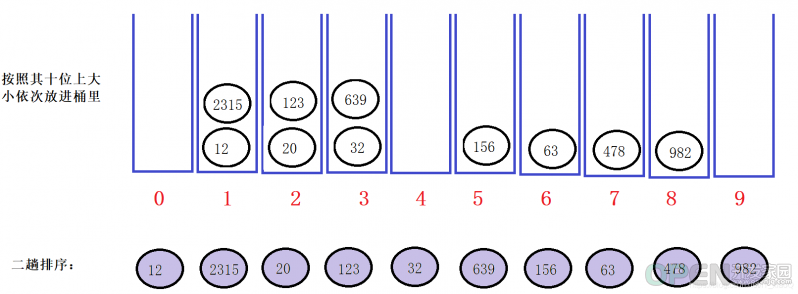
第二次排序我将所有数据按照其十位上的大小进行排序依次放进桶中，并且将排序完成后的重新放回原位置上。

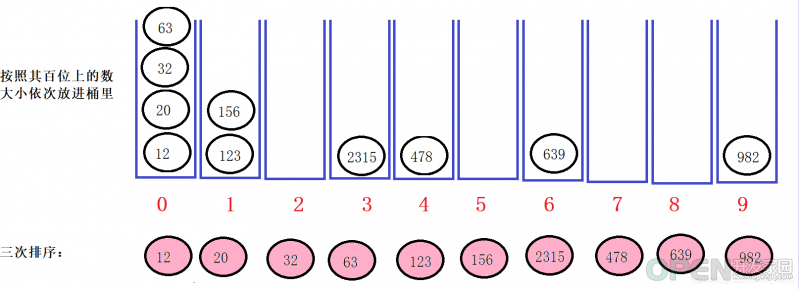
第三次排序我将所有数据按照其百位上的大小进行排序依次放进桶中，并且将排序完成后的重新放回原位置上。

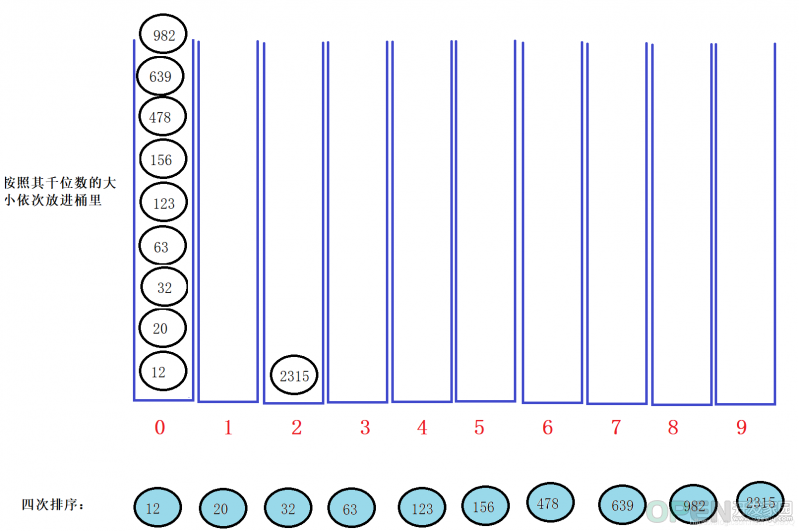
四次循坏完成后，这一组数据也就排序完成。

代码实现：

#pragma once
//基数排序
//1.按照低位优先开始
//6 8 9 2 4 1 3 7
#include<stdlib.h>
#include<cmath>
#include<iostream>
using namespace std;
//1.打印排序后的数组
void PrintArray(int array[], int size);
//2.交换两个数
void Swap(int* num1, int* num2);
//3.数组中最大的数
int MaxNum(int array[], int size);
//4.最大的数有多少位，记录其位数
int MaxWeiShu(int num);
//5.将基数进行一次排序
void OneSort(int array[], int size, int i);
//6.基数排序
void RadixSort(int array[], int size);

#include"RadixSort.h"
//打印排序后的数组
void PrintArray(int array[], int size)
{
  for (int y = 0; y < size; y++)
  {
  cout << array[y] << " ";
  }
  cout << endl;
}
//2.交换两个数
void Swap(int* num1, int* num2)
{
  int temp = *num1;
  *num1 = *num2;
  *num2 = temp;
}
// { 12,63,156,982,20,478,639,32,2315,123 };
//3.数组中最大的数
int MaxNum(int array[], int size)
{
  int temp = array[0];
  for (int i = 1; i < size; i++)
  {
  if (array[i] > temp)
  {
    temp = array[i];
  }
  }
  return temp;
}
//4.最大的数有多少位，记录其位数
int MaxWeiShu(int num)
{
  int counts = 0;
  while (1)
  {
  if (num / 10 != 0)
  {
    num = num / 10;
    counts++;
  }
  else
  {
    break;
  }
  }
  return counts + 1;
}
//5.将基数进行一次排序
void OneSort(int array[], int size, int i)
{
  //记录每个桶中存放的个数
  int arrk[10] = { 0 };
  //创建10个桶
  int arr[10][10000] = {0};
  //将所有数进行存放进桶中
  for (int j = 0; j < size; j++)
  {
  //判断每一个数不同位上的数
  int temp = (int)(array[j] / pow(10, i)) % 10;
  //cout << temp << endl;
  //判断归类的数在哪个桶中，并放进去
  for (int OneNum = 0; OneNum < 10; OneNum++)
  {
    if (temp == OneNum)
    {
    arr[OneNum][arrk[OneNum]] = array[j];
    arrk[OneNum] += 1;
    break;
    }
  }
  }
  int as = 0;
  //将每一次排序后的数重新放回原数组
  for (int OneNum = 0; OneNum < 10; OneNum++)
  {
  //将每个桶中的数依次在放回原数组
  for (int x = 0; x < arrk[OneNum]; x++)
  {
    array[as] = arr[OneNum][x];
    as++;
  }
  }
}
//6.基数排序
void RadixSort(int array[], int size)
{
  if (size <= 1)
  {
  return;
  }
  //数组中最大的数
  int Max = MaxNum(array, size);
  //最大的数有多少位，记录其位数
  int count = MaxWeiShu(Max);
  //取出每个数的每个位数按其大小进行排序
  for (int i = 0; i < count; i++)
  {
  //一次排序之后的顺序
  OneSort(array, size, i);
  }
}

#include"RadixSort.h"
#include<ctime>
#include<Windows.h>
#define SIZE 10000
int main()
{
  //srand((unsigned int)time(NULL));
  //int array[SIZE];
  //for (int i = 0; i < SIZE; i++)
  //{
  //  array[i] = rand() % 1000000;
  //}
  //cout << "未排序:";
  //Sleep(1000);
  //PrintArray(array, SIZE);
  //Sleep(1000);
  //RadixSort(array, SIZE);
  //cout << "已排序:";
  //Sleep(1000);
  //PrintArray(array, SIZE);
  int array[]= { 12,63,156,982,20,478,639,32,2315,123 };
  int size = sizeof(array) / sizeof(array[0]);
  PrintArray(array, size);
  RadixSort(array, size);
  PrintArray(array, size);
  system("pause");
  return 0;
}

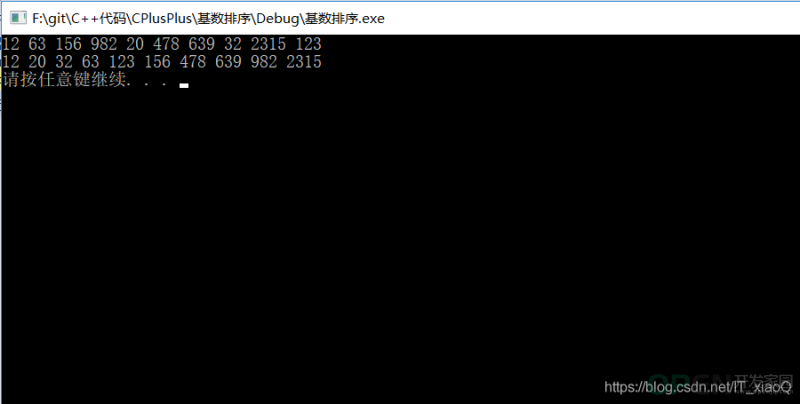
结果显示：

基数排序的时间复杂度：O (nlog(r)m)，其中r是所采取的基数，而m是堆数。由于这种排序只针对整数，所以局限性较大。但效率高。
珍&源码